
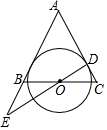
 如图,在△ABC中,AB=AC,点O为BC中点,⊙O与AC相切于点D,连接DO并延长,与AB的延长线相交于点E.
如图,在△ABC中,AB=AC,点O为BC中点,⊙O与AC相切于点D,连接DO并延长,与AB的延长线相交于点E.分析 (1)连接OA,作OF⊥AB于F,如图,由切线的性质得OD⊥AC,再根据等腰三角形的性质得AO平分∠BAC,根据角平分线的性质得OF=OD,然后根据切线的判定定理即可得到AB为⊙O的切线;
(2)先证明△EBO∽△EOA,利用相似比可计算出OE=$\frac{10}{3}$,再证明Rt△EOF∽Rt△EAD得到$\frac{OF}{AD}$=$\frac{OE}{EA}$=$\frac{1}{2}$,则设⊙O的半径为r,则AD=2r,AF=2r,BF=5-2r,然后利用射影定理得到OF2=AF•BF,即r2=2r•(5-2r),再解方程求出r即可.
解答 解:(1)⊙O与AB相切.理由如下:
连接OA,作OF⊥AB于F,如图,
∵⊙O与AC相切于点D,
∴OD⊥AC,
∵AB=AC,点O为BC中点,
∴AO平分∠BAC,
∴OF=OD,
∴AB为⊙O的切线;
(2)∵AB=AC,点O为BC中点,
∴OA⊥BC,
∴∠3+∠C=90°,
∵∠2+∠C=90°,
∴∠2=∠3,
而∠1=∠2,∠3=∠OAB,
∴∠1=∠OAB,
而∠BEO=∠OEA,
∴△EBO∽△EOA,
∴EO:EA=EB:EO,即EO2=EB•EA=$\frac{5}{3}$($\frac{5}{3}$+5)=$\frac{10}{3}$,
∵∠OEF=∠AED,
∴Rt△EOF∽Rt△EAD,
∴$\frac{OF}{AD}$=$\frac{OE}{EA}$=$\frac{\frac{10}{3}}{\frac{5}{3}+5}$=$\frac{1}{2}$,
设⊙O的半径为r,则AD=2r,AF=2r,BF=5-2r,
∵OF⊥AB,
∴OF2=AF•BF,即r2=2r•(5-2r),解得r=$\sqrt{2}$,
∴⊙O的半径为$\sqrt{2}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.会运用相似比计算线段的长.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:选择题
| A. | -m8n4 | B. | mn4 | C. | -m9n | D. | 5m3n2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 药品研究所开发一种抗菌新药,经过多年的动物实验后,首次用于临床人体试验,测得成人服药后血液中的药物浓度y(μg/ml)与服药后时间x(h)之间的函数关系如图所示,则当1≤x≤6时,y的取值范围是( )
药品研究所开发一种抗菌新药,经过多年的动物实验后,首次用于临床人体试验,测得成人服药后血液中的药物浓度y(μg/ml)与服药后时间x(h)之间的函数关系如图所示,则当1≤x≤6时,y的取值范围是( )| A. | $\frac{8}{3}$≤y≤$\frac{64}{11}$ | B. | $\frac{64}{11}$≤x≤8 | C. | $\frac{8}{3}$≤y≤8 | D. | 8≤x≤16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | -1 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
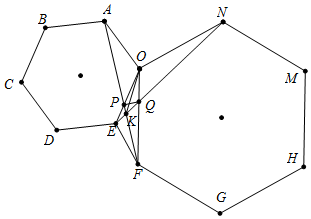 如图所示:以△OEF的两边OE,OF为边向外作两个正六边形,正六边形OABCDE,正六边形OFGHMN.则下列结论正确的是:①△EON≌△AOF;②∠AKE=90°;③△PKQ为等边三角形;④PQ∥EF;⑤OK平分∠EOF,则下列选项正确的是( )
如图所示:以△OEF的两边OE,OF为边向外作两个正六边形,正六边形OABCDE,正六边形OFGHMN.则下列结论正确的是:①△EON≌△AOF;②∠AKE=90°;③△PKQ为等边三角形;④PQ∥EF;⑤OK平分∠EOF,则下列选项正确的是( )| A. | ①、②、③、④、⑤ | B. | ②、③、④ | C. | ①、⑤ | D. | ③、④、⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
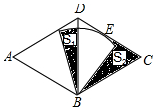 如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1,S2,则S2-S1=2$\sqrt{3}$-π.
如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1,S2,则S2-S1=2$\sqrt{3}$-π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,对称轴为直线x=$\frac{7}{2}$的抛物线经过点A(6,0)和B(0,4)
如图,对称轴为直线x=$\frac{7}{2}$的抛物线经过点A(6,0)和B(0,4)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com