
【题目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
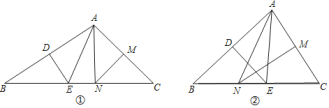
(1)请判断△ANE的周长与AB+AC的和的大小,并说明理由.
(2)①如图①,若∠B=34°,∠C=28°,求![]() 的度数为______;
的度数为______;
②如图②,若![]() ,则
,则![]() 的度数为________;
的度数为________;
③若![]()
![]() ,则
,则![]() 的度数为________.
的度数为________.
【答案】(1)△ANE的周长<AB+BC;(2)①56°;②16°;③当0°<α<90°时,∠EAN=180°-2α;当180°>α>90°时,∠EAN=2α-180°
【解析】
(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,AN=CN,则△ANE的周长等于BE+EN+AN;
(2)①根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,再根据等边对等角可得∠BAE=∠B,同理可得,∠CAN=∠C,然后利用外角和公式求出∠EAN=180°-2∠B-2∠C,即可求解;
②根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,再根据等边对等角可得∠BAE=∠B,同理可得,∠CAN=∠C,然后利用三角形的内角和定理求出∠B+∠C,再根据∠EAN=∠BAC-(∠BAE+∠CAN)代入数据进行计算即可得解;
③根据前两问的求解方法,分0°<α<90°与180°>α>90°两种情况解答.
解:(1)△ANE的周长<AB+BC,理由如下
∵DE垂直平分AB,![]() 垂直平分
垂直平分![]()
∴AE=BE,AN=CN
又∵△ANE的周长=AE+EN+AN
∴△ANE的周长=AE+EN+AN=BE+EN+CN=BC
∴△ANE的周长<AB+BC
(2)①∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
在三角形AEN中,
∴∠EAN=180°-∠AEN-∠ANE,
又∵∠AEN=∠B+∠BAE, ∠ANE=∠C+∠CAN
∴∠EAN=180°-2∠B-2∠C=56°;
②∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN-∠BAC,
=(∠B+∠C)-∠BAC,
在△ABC中,∠B+∠C=180°-∠BAC=98°,
∴∠EAN=∠BAE+∠CAN-∠BAC=98°-82°=16°;
③∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN-∠BAC,
=(∠B+∠C)-∠BAC,
在△ABC中,∠B+∠C=180°-∠BAC=180°-α,
∴∠EAN=∠BAE+∠CAN-∠BAC=![]() -α=180°-2α
-α=180°-2α
∴当0°<α<90°时,∠EAN=180°-2α;
当180°>α>90°时,∠EAN=2α-180°.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】小李家住房结构如图所示,小李打算把卧室和客厅铺上木地板.
(1)请问他至少需要买多少平方米的木地板?(用字母表示)
(2)若![]() 米,
米,![]() 米时,并且每平方米木地板的价格是
米时,并且每平方米木地板的价格是![]() 元,则他至少需要准备多少元钱?
元,则他至少需要准备多少元钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P为∠AOB的角平分线上的一点,点D在边OA上.在边OB上取一点E,使得PE=PD.
(1)用圆规作出所有符合条件的点E;
(2)写出∠OEP与∠ODP的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
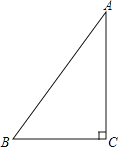
【题目】如图,![]() 中,∠C=90°,
中,∠C=90°,![]() ,
,![]() ,若动点P从点C开始,按
,若动点P从点C开始,按![]() 的路径运动,且速度为每秒1cm,设出发的时间为t秒.
的路径运动,且速度为每秒1cm,设出发的时间为t秒.
![]() 点P出发2秒后,求CP和BP的长.
点P出发2秒后,求CP和BP的长.
![]() 问t满足什么条件时
问t满足什么条件时![]() 的值或取值范围
的值或取值范围![]() ,
,![]() 为直角三角形?
为直角三角形?
![]() 另有一点Q,从点C开始,按
另有一点Q,从点C开始,按![]() 的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动
的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动![]() 当t为何值时,直线PQ把
当t为何值时,直线PQ把![]() 的周长分成相等的两部分?
的周长分成相等的两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
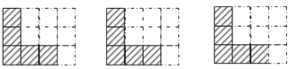
【题目】(1)如图,阴影部分是由5个小正方形组成的一个直角图形,请用3种方法分别在下图方格内添涂黑二个小正方形,使阴影部分成为轴对称图形.
(2)如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
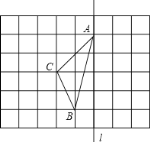
①在图中画出与△ABC关于直线l成轴对称的△AB′C′;
②△ABC的面积为____________;
③在直线l上找一点P,使PB+PC的长最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90.
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 .
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
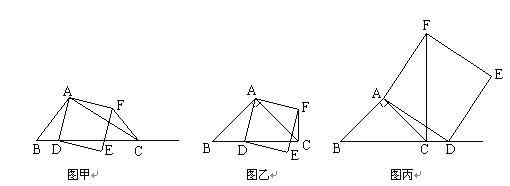
(2)如果AB≠AC,∠BAC≠90,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?画出相应图形,并说明理由.(画图不写作法)
(3)若AC=![]() ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上![]() ,
,![]() 两点对应数分别为-3,20.
两点对应数分别为-3,20.
(1)若![]() 点为线段
点为线段![]() 的中点,求
的中点,求![]() 点对应的数.
点对应的数.
(2)若点![]() 以每秒3个单位,点
以每秒3个单位,点![]() 以每秒2个单位的速度同时出发向右运动多长时间后
以每秒2个单位的速度同时出发向右运动多长时间后![]() ,
,![]() 两点相距2个单位长度?
两点相距2个单位长度?
(3)若点![]() ,
,![]() 同时分别以2个单位长度秒的速度相向运动,点
同时分别以2个单位长度秒的速度相向运动,点![]() (
(![]() 点在原点)同时以4个单位长度/秒的速度向右运动.
点在原点)同时以4个单位长度/秒的速度向右运动.
①经过![]() 秒后
秒后![]() 与
与![]() 之间的距离
之间的距离![]() (用含
(用含![]() 的式子表示)
的式子表示)
②几秒后点![]() 到点
到点![]() 、点
、点![]() 的距离相等?求此时
的距离相等?求此时![]() 对应的数.
对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线,E是AB上一点,且AE=AD,连接ED,作EF⊥BD于F,连接CF.则下面的结论:
①CD=CF;
②∠EDF=45°;
③∠BCF=45°;
④若CD=4,AD=5,则S△ADE=10.其中正确结论的个数是( )
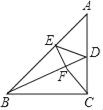
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com