
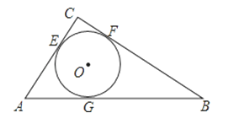
【题目】在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.
(1)求证:内切圆的半径r=1;
(2)求tan∠OAG的值.
科目:初中数学 来源: 题型:
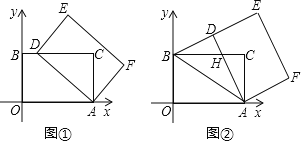
【题目】附加题:(1)已知:如图①,在![]() 和
和![]() 中,OA=OB,OC=OD,
中,OA=OB,OC=OD,![]() ,求证:①AC=BD;②
,求证:①AC=BD;②![]() .
.
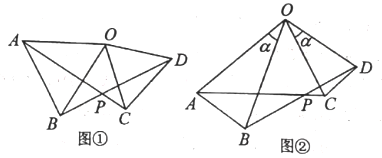
(2)如图②,在![]() 和
和![]() 中,若OA=OB,OC=OD,
中,若OA=OB,OC=OD,![]() ,则AC与BD间的等量关系式为 ;
,则AC与BD间的等量关系式为 ;![]() 的大小为 .
的大小为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝新中国成立70周年,某校组织八年级全体学生参加“恰同学少年,忆峥嵘岁月”新中国成立70周年知识竞赛活动.将随机抽取的部分学生成绩进行整理后分成5组,50~60分(![]() )的小组称为“学童”组,60~70分(
)的小组称为“学童”组,60~70分(![]() )的小组称为“秀才”组,70~80分(
)的小组称为“秀才”组,70~80分(![]() )的小组称为“举人”组,80~90分(
)的小组称为“举人”组,80~90分(![]() )的小组称为“进士”组,90~100分(
)的小组称为“进士”组,90~100分(![]() )的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题:
)的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题:
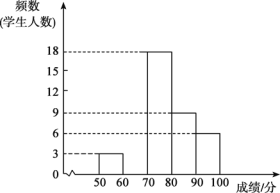
(1)若“翰林”组成绩的频率是12.5%,请补全频数分布直方图;
(2)在此次比赛中,抽取学生的成绩的中位数在 组;
(3)学校决定对成绩在70~100分(![]() )的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖?
)的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
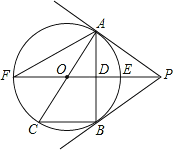
(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF、OD、OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F=![]() ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与○O相交于点D,连接BD,则∠DBC的大小为

A. 15° B. 35° C. 25° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.
(1)如图①,当点D落在BC边上时,求点D的坐标;
(2)如图②,当点D落在线段BE上时,AD与BC交于点H.
①求证△ADB≌△AOB;
②求点H的坐标.
(3)记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.

(1)求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;
(2)求出a的值;
(3)求张师傅途中加油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b,那么(a+b)2的值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com