
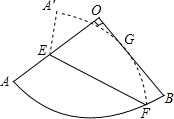
 如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A'F}$恰好与半径OB相切于点G.若OE=4,则O到折痕EF的距离为2$\sqrt{3}$.
如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A'F}$恰好与半径OB相切于点G.若OE=4,则O到折痕EF的距离为2$\sqrt{3}$. 分析 过点G作O′G⊥OB,作AO′⊥O′G于O′,如图,连结OO′交EF于H,易得四边形AOGO′为矩形,得到O′G=AO=5,根据折叠的性质得$\widehat{AF}$与$\widehat{A′F}$为等弧,则它们所在圆的半径相等,再利用经过切点且垂直于切线的直线必经过圆心得到点O′为$\widehat{A′F}$所在圆的圆心,则可判断点O与点O′关于EF对称,所以OO′⊥EF,OH=HO′,设OH=x,则OO′=2x,接着证明Rt△OEH∽Rt△OO′A,然后利用相似比可计算出x.
解答  解:过点G作O′G⊥OB,作AO′⊥O′G于O′,如图,连结OO′交EF于H,
解:过点G作O′G⊥OB,作AO′⊥O′G于O′,如图,连结OO′交EF于H,
则四边形AOGO′为矩形,
∴O′G=AO=6,
∵$\widehat{AF}$沿EF折叠后所得得圆弧$\widehat{A′F}$恰好与半径OB相切于点G,
∴$\widehat{AF}$与$\widehat{A′F}$所在圆的半径相等,
∴点O′为$\widehat{A′F}$所在圆的圆心,
∴点O与点O′关于EF对称,
∴OO′⊥EF,OH=HO′,
设OH=x,则OO′=2x,
∵∠EOH=∠O′OA,
∴Rt△OEH∽Rt△OO′A,
∴$\frac{OH}{OA}$=$\frac{OE}{OO′}$,即$\frac{x}{6}$=$\frac{4}{2x}$,解得x=2$\sqrt{3}$,
即O到折痕EF的距离为2$\sqrt{3}$.
故答案为2$\sqrt{3}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点;经过切点且垂直于切线的直线必经过圆心.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了折叠的性质.


科目:初中数学 来源: 题型:解答题
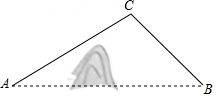 A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
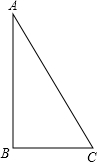 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的底面圆的周长分别记作l1,l2,侧面积分别记作S1,S2,则( )
如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的底面圆的周长分别记作l1,l2,侧面积分别记作S1,S2,则( )| A. | l1:l2=1:2,S1:S2=1:2 | B. | l1:l2=1:4,S1:S2=1:2 | ||
| C. | l1:l2=1:2,S1:S2=1:4 | D. | l1:l2=1:4,S1:S2=1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | c<b<a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com