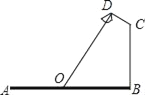
【题目】如图，要在宽为22米的九州大道两边安装路灯，路灯的灯臂CD长2米，且与灯柱BC成120°角，路灯采用圆锥形灯罩，灯罩的轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线时照明效果最佳，此时，路灯的灯柱BC高度应该设计为（ ）
A. （11﹣2
）米 B. （11
﹣2
）米 C. （11﹣2
）米 D. （11
﹣4）米
培优好卷单元加期末卷系列答案科目：初中数学 来源： 题型：
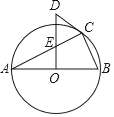
【题目】如图，△ABC内接于⊙O，且AB为⊙O的直径OD⊥AB，与AC交于点E，与过点C的⊙O切线交于点D．
（1）若AC=6，BC=3，求OE的长．
（2）试判断∠A与∠CDE的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
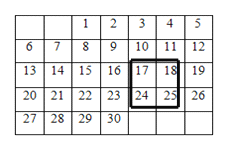
【题目】仔细观察下面的日历，回答下列问题：
（1）任意用正方形框圈出四个日期，如果正方形框中的第一个数（左上角的数）为
，用代数式表示正方形框中的四个数的和；
（2）若将正方形框上下左右移动，可框住另外的四个数，这四个数的和能等于
吗？如果能，依次写出这四个数；如果不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
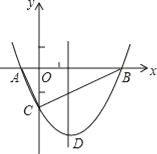
【题目】如图，抛物线y=
x2+bx﹣2与x轴交于A、B两点，与y轴交于C点，且A（一1，0）．
（1）求抛物线的解析式及顶点D的坐标；
（2）判断△ABC的形状，证明你的结论；
（3）点M是抛物线对称轴上的一个动点，当△ACM周长最小时，求点M的坐标及△ACM的最小周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=AC，AD是∠BAC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE.
（1）求证：四边形AEBD是矩形；
（2）当∠BAC= 时，矩形AEBD是正方形.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】提出问题：“周长一定的长方形，当邻边长度满足什么条件时面积最大？”
探究发现：如图所示，小敏用4个完全相同的、邻边长度分别为a、b的长方形拼成一个边长为（a+b）的正方形（其中a、b的和不变，但a、b的数值及两者的大小关系都可以变化）．仔细观察拼图，我们发现，如果右图中间有空白图形F，那么它一定是正方形
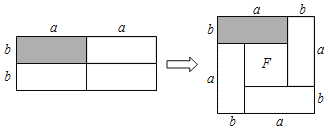
（1）空白图形F的边长为 ；
（2）通过计算左右两个图形的面积，我们发现（a+b）2、（a﹣b）2和ab之间存在一个等量关系式．
①这个关系式是 ；
②已知数x、y满足：x+y＝6，xy＝
，则x﹣y＝ ；
问题解决：
问题：“周长一定的长方形，当邻边长度满足什么条件时面积最大？”
①对于周长一定的长方形，设周长是20，则长a和宽b的和是 面积S＝ab的最大值为 ，此时a、b的关系是 ；
②对于周长为L的长方形，面积的最大值为 ．
活动经验：
周长一定的长方形，当邻边长度a、b满足 时面积最大．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下表是小华同学一个学期数学成绩的记录．根据表格提供的信息，回答下列的问题：
考试类别 | 平时考试 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩（分） | 85 | 78 | 90 | 91 | 90 | 94 |
（1）小明6次成绩的众数是 ，中位数是 ；
（2）求该同学这个同学这一学期平时成绩的平均数；
（3）总评成绩权重规定如下：平时成绩占20%，期中成绩占30%，期末成绩占50%，请计算出小华同学这一个学期的总评成绩是多少分？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠BAC的平分线与BC的中垂线DE交于点E，过点E作AC边的垂线，垂足为N，过点E作AB延长线的垂线，垂足为M.
(1)求证：BM=CN；
(2)若，AB=2，AC=8，求BM的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
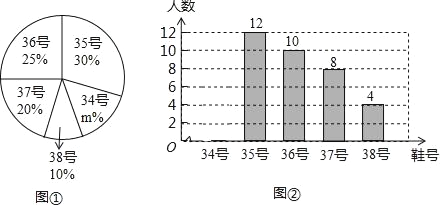
【题目】为了方便学生参加体育锻炼，某学校准备购买一批运动鞋供学生体育锻炼借用．现从各年级随机抽取了部分学生的鞋号，绘制出如下不完整的统计图①和图②，请根据有关信息，解答下列问题：
（1）填空：本次随机抽样调查的学生为 名，本次调查获取的样本数据的中位数是 号，众数是 号；
（2）补全条形统计图；
（3）根据样本数据，若学校计划购买800双运动鞋，建议购买34号运动鞋多少双？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
