
【题目】如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是 . 随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是 . 
【答案】( ![]() ,1);y=
,1);y= ![]() x﹣2
x﹣2
【解析】解:如图,过点C′作C′F⊥x轴于点F,
∵△AOC′是等边三角形,OA=2,
∴C′F=1.
在Rt△OC′F中,
由勾股定理,得OF= ![]() =
= ![]() =
= ![]() .
.
∴点C′的坐标为( ![]() ,1).
,1).
∵△AOC′与△ABC都是等边三角形,
∴AO=AC′,AB=AC,∠BAC=∠OAC′=60°,
∴∠BAC﹣∠OAC=∠OAC′﹣∠OAC,
∴∠BAO=∠CAC′,
在△AOB与△AC′C中,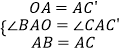
∴△AOB≌△AC′C(SAS).
∴∠BOA=∠CC′A=90°,
∴点C在过点C′且与AC垂直的直线上,
∵点A的坐标是(0,2),△ABC是等边三角形,
∴点C移动到y轴上的坐标是(0,﹣2),
设点C所在的直线方程为:y=kx+b(k≠0).把点( ![]() ,1)和(0,﹣2)分别代入,得
,1)和(0,﹣2)分别代入,得 ![]() ,
,
解得 ![]() ,
,
所以点C移动所得图象的解析式是为:y= ![]() x﹣2.
x﹣2.
所以答案是( ![]() ,1),y=
,1),y= ![]() x﹣2.
x﹣2.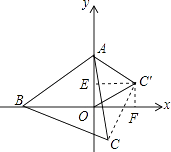


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD. 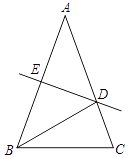
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
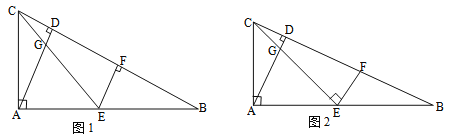
【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
(1)如图1,若AC:AB=1:2,EF⊥CB,求证:EF=CD;
(2)如图2,若AC:AB=1: ![]() ,EF⊥CE,求EF: EG的值.
,EF⊥CE,求EF: EG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们不妨把纵坐标是横坐标的2倍的点称为“理想点”.例如点(﹣2,﹣4),(1,2),(3,6)…都是“理想点”,显然这样的“理想点”有无数多个.
(1)若点M(2,a)是“理想点”,且在正比例函数y=kx(k为常数,k≠0)图象上,求这个正比例函数的表达式.
(2)函数y=3mx﹣1(m为常数,且m≠0)的图象上存在“理想点”吗?若存在,请用含m的代数式表示出“理想点”的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com