
【题目】如图,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )

A. 1个 B. 4个 C. 3个 D. 2个
【答案】C
【解析】∵D是BC的中点,且DE⊥BC,
∴DE是BC的垂直平分线,CD=BD,
∴CE=BE,故本答案正确;
∴∠C=∠7
∵AD=AB,
∴∠8=∠ABC=∠6+∠7,
∵∠8=∠C+∠4,
∴∠C+∠4=∠6+∠7,
∴∠4=∠6,即∠CAD=∠ABE,故本答案正确;
作AG⊥BD于点G,交BE于点H,
∵AD=AB,DE⊥BC,
∴∠2=∠3,DG=BG=![]() BD,DE∥AG,
BD,DE∥AG,
∴CDE△∽△CGA,△BGH∽△BDE,EH=BH,∠EDA=∠3,∠5=∠1,
∴CD:CG=DE:AG,HG=![]() DE,
DE,
设DG=x,DE=y,则GB=x,CD=2x,CG=3x
∴2x:3x=2y:AG,
解得:AG=3y,HG=y
∴AH=2y
∴DE=AH,且∠EDA=∠3,∠5=∠1
∴DEF△≌△AHF
∴EF=HF=![]() EH,且EH=BH,
EH,且EH=BH,
∴EF:BF=1:3,
∴S△ABF=3S△AEF,
∵S△DEF=S△AEF,
∴S△ABF=3S△DEF,故本答案正确;
∵∠1=∠2+∠6,且∠4=∠6,∠2=∠3,
∴∠5=∠3+∠4,
∴∠5≠∠4,
∴△DEF∽△DAE,不成立,故本答案错误,
综上所述:正确的答案有3个,
故选C.



 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
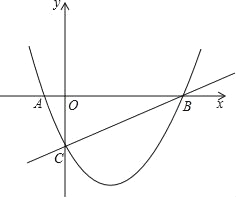
【题目】如图,已知抛物线y=ax2﹣![]() x+c与x轴相交于A、B两点,并与直线y=
x+c与x轴相交于A、B两点,并与直线y=![]() x﹣2交于B、C两点,其中点C是直线y=
x﹣2交于B、C两点,其中点C是直线y=![]() x﹣2与y轴的交点,连接AC.
x﹣2与y轴的交点,连接AC.
(1)求抛物线的解析式;
(2)证明:△ABC为直角三角形;
(3)△ABC内部能否截出面积最大的矩形DEFG?(顶点D、E、F、G在△ABC各边上)若能,求出最大面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
(1)求证:四边形ADBE是矩形;
(2)连接DE,交AB与点O,若BC=8,AO=3,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
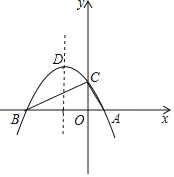
【题目】如图,抛物线y=﹣![]() x2+bx+2与x轴交于A,B两点,与y轴交于C点,且点A的坐标为(1,0).
x2+bx+2与x轴交于A,B两点,与y轴交于C点,且点A的坐标为(1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,并证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车公司有甲、乙两种货车可供租用,现有一批货物要运往某地,货主准备租用该公司货车,已知以往甲、乙两种货车运货情况如下表:

(1)甲、乙两种货车每辆可装多少吨货物?
(2)若货主需要租用该公司的甲种货车8辆,乙种货车6辆,刚好运完这批货物,如按每吨付运费50元,则货主应付运费总额为多少元?
(3)若货主共有20吨货,计划租用该公司的货车正好(每辆车都满载)把这批货运完,该汽车公司共有哪几种运货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
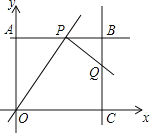
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.
(1)求点B的坐标;
(2)当点P在线段AB上运动(不与A,B重合)时,设点P的横坐标为m,线段CQ的长度为l.求出l关于m的函数解析式;
(3)在坐标平面内是否存在点D,使以O、P、Q、D为顶点的四边形为正方形?若存在,请直接写出D点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,线段AB上有两个点C、D,请计算图中共有多少条线段?
![]()
(2)如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?
(3)拓展应用:8个班级参加学校组织的篮球比赛,比赛采用单循环制(即每两个班级之间都要进行一场比赛),那么一共要进行多少场比赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,E为CA延长线上一点,D为AB上一点,F为
,E为CA延长线上一点,D为AB上一点,F为![]() 外一点且
外一点且![]() 连接DF,BF.
连接DF,BF.
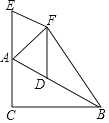
(1)当![]() 的度数是多少时,四边形ADFE为菱形,请说明理由:
的度数是多少时,四边形ADFE为菱形,请说明理由:
(2)当AB= 时,四边形ACBF为正方形(请直接写出)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com