
分析 (1)根据☆的含义,以及有理数的混合运算的运算方法,求出(-2)☆5的值是多少即可.
(2)根据☆的含义,可得$\frac{a+1}{2}$☆3=$\frac{a+1}{2}$×32-2×$\frac{a+1}{2}$×3+$\frac{a+1}{2}$=8,据此求出a的值是多少即可.
(3)首先根据☆的含义,以及m=2☆x,n=(1-x)☆3(其中x为有理数),分别求出m、n的值各是多少;然后比较大小即可.
解答 解:(1)(-2)☆5
=(-2)×52-2×(-2)×5+(-2)
=-50+20-2
=-32;
(2)$\frac{a+1}{2}$☆3
=$\frac{a+1}{2}$×32-2×$\frac{a+1}{2}$×3+$\frac{a+1}{2}$
=4.5a+4.5-3a-3+0.5a+0.5
=2a+2
=8
解得:a=3;
(3)m=2☆x
=2x2-2×2x+2
=2x2-4x+2
n=(1-x)☆3
=(1-x)×32-2×(1-x)×3+(1-x)
=9-9x-6+6x+1-x
=4-4x
∵m-n=(2x2-4x+2)-(4-4x)
=2x2-2,
当x>1或x<-1时,2x2-2>0,即m>n,
当x=±1时,2x2-2=0,即m=n
当-1<x<1时,2x2-2<0,即m<n,
故答案为:>或=或<.
点评 此题主要考查了定义新运算,以及有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 50 | C. | 10或50 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
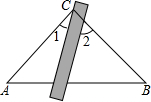 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=67°,则∠1的度数为( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=67°,则∠1的度数为( )| A. | 33° | B. | 23° | C. | 67° | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
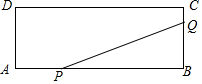 如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com