
| a1,1 | a1,2 | a1,3 | a1,4 |
| a2,1 | a2,2 | a2,3 | a2,4 |
| a3,1 | a3,2 | a3,3 | a3,4 |
| a4,1 | a4,2 | a4,3 | a4,4 |
| 问题1 | 问题2 |
| a2,1•ai,j+a2,2•ai,j+a2,3•ai,j+a2,4•ai,j=0或3; | 表中的16个数中,共有10个1. |
分析 (1)根据定义当i≤j时,ai,j=1可得;
(2)问题1:分i>j和i≤j,依据定义分别代入数值求解可得;
问题2:表中的16个数中,值为1的有:a1,1、a1,2、a1,3、a1,4、a2,2、a2,3、a2,4、a3,3、a3,4、a4,4,即可得出答案.
解答 解:(1)∵a1,3中1<3,
∴a1,3=1,
故答案为:1;
(2)问题1:若i>j,则a2,1•ai,j+a2,2•ai,j+a2,3•ai,j+a2,4•ai,j=0×0+1×0+1×0+1×0=0,
若i≤j,则a2,1•ai,j+a2,2•ai,j+a2,3•ai,j+a2,4•ai,j=0×1+1×1+1×1+1×1=3,
∴a2,1•ai,j+a2,2•ai,j+a2,3•ai,j+a2,4•ai,j=0或3,
故答案为:0或3;
问题2:表中的16个数中,值为1的有:a1,1、a1,2、a1,3、a1,4、a2,2、a2,3、a2,4、a3,3、a3,4、a4,4,
∴表中的16个数中,共有10个;
故答案为:10.
点评 本题主要考查数字的变化类,依据题意弄清规定:当i>j时,ai,j=0;当i≤j时,ai,j=1是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
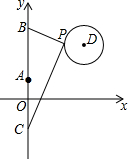 如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1-t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是$\sqrt{13}$-1.
如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1-t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是$\sqrt{13}$-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com