
【题目】已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).
①画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是 ;
②以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1 ,点C2的坐标是 ;
③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标 .
【答案】(2,-2);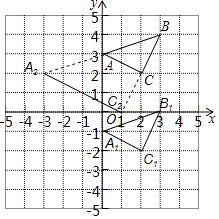 ;(1,0); (2a﹣3,2b﹣4)
;(1,0); (2a﹣3,2b﹣4)
【解析】解:①如图所示:△A1B1C1,即为所求,点C1的坐标是:(2,﹣2);
所以答案是:(2,﹣2);
②如图所示:△A2BC2,即为所求,点C2的坐标是:(1,0);
所以答案是:(1,0);
③若M(a,b)为线段AC上任一点,
则点M的对应点M2的坐标为:(2a﹣3,2b﹣4).
所以答案是:(2a﹣3,2b﹣4).
【考点精析】认真审题,首先需要了解作图-位似变换(对应点到位似中心的距离比就是位似比,对应线段的比等于位似比,位似比也有顺序;已知图形的位似图形有两个,在位似中心的两侧各有一个.位似中心,位似比是它的两要素).


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】母亲节前夕,某淘宝店主从厂家购进A、B两种礼盒,已知A、B两种礼盒的单价比为2:3,单价和为200元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该店主购进这两种礼盒恰好用去9600元,且购进A种礼盒最多36个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)根据市场行情,销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元.为奉献爱心,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,m值是多少?此时店主获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.
(1)若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN°.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD边上的一动点,它从点A出发沿着A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为 ![]() 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.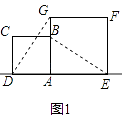
(1)图1中,小明发现DG=BE,请你帮他说明理由.
(2)小明将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,请你直接写出此时BE的长.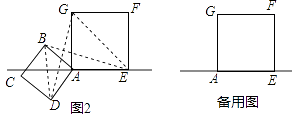
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,一次函数
,一次函数![]() 的图像分别与
的图像分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,且与
,且与![]() 的图像交于点
的图像交于点![]() .
.

(1)求![]() 的值;
的值;
(2)若![]() ,则
,则![]() 的取值范围是 ;
的取值范围是 ;
(3)求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com