
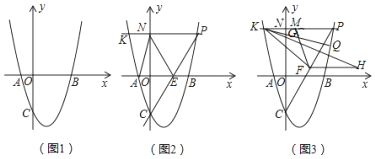
【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c交x轴于A(﹣1,0),B(3,0)两点,交y轴于点C.
(1)如图1,求抛物线的解析式;
(2)如图2,点P是第一象限抛物线上的一个动点,连接CP交x轴于点E,过点P作PK∥x轴交抛物线于点K,交y轴于点N,连接AN、EN、AC,设点P的横坐标为t,四边形ACEN的面积为S,求S与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,点F是PC中点,过点K作PC的垂线与过点F平行于x轴的直线交于点H,KH=CP,点Q为第一象限内直线KP下方抛物线上一点,连接KQ交y轴于点G,点M是KP上一点,连接MF、KF,若∠MFK=∠PKQ,MP=AE+![]() GN,求点Q坐标.
GN,求点Q坐标.
【答案】(1)y=x2﹣2x﹣3;(2)S=![]() t2+
t2+![]() t;(3)Q(
t;(3)Q(![]() ,
,![]() ).
).
【解析】
(1)函数的表达式为:y=(x+1)(x﹣3),即可求解;
(2)tan∠PCH=![]() =
=![]() =
=![]() ,求出OE=
,求出OE=![]() ,利用S=S△NCE+S△NAC,即可求解;
,利用S=S△NCE+S△NAC,即可求解;
(3)证明△CNP≌△KRH,求出点P(4,5)确定tan∠QKP=![]() =
=![]() =4﹣m=tan∠QPK=
=4﹣m=tan∠QPK=![]() =
=![]() NG,最后计算KT=MT=
NG,最后计算KT=MT=![]() (
(![]() ),FT=4
),FT=4![]() ﹣
﹣![]() (
(![]() +
+![]() ),tan∠MFT=
),tan∠MFT= =4﹣m,即可求解.
=4﹣m,即可求解.
(1)函数的表达式为:y=(x+1)(x﹣3)=x2﹣2x﹣3;
(2)过点P作PH⊥y轴交于点H,设点P(t,t2﹣2t﹣3),
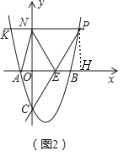
CN=t2﹣2t﹣3+3=t2﹣2t,
∴tan∠PCH=![]() =
=![]() =
=![]() ,
,
![]() ,解得:OE=
,解得:OE=![]() ,
,
S=S△NCE+S△NAC=![]() AE×CN=
AE×CN=![]() t2+
t2+![]() t;
t;
(3)过点K作KR⊥FH于点R,
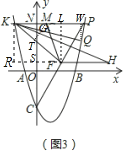
∵KH=CP,∠NCP=∠H,∠R=∠PNC=90°,
∴△CNP≌△KRH,∴PN=KR=NS,
∵点F是PC中点,SF∥NP,
∴PN=KR=NS=![]() CN,即t=
CN,即t=![]() (t2﹣2t﹣3+3),
(t2﹣2t﹣3+3),
解得:t=0或4(舍去0),点P(4,5),
点K、P时关于对称轴的对称点,故点K(﹣2,5),
∵OE∥PN,则![]() ,故OE=
,故OE=![]() ,同理AE=
,同理AE=![]() ,
,
设点Q(m,m2﹣2m﹣3),过点Q作WQ⊥KP于点W,
WQ=5﹣(m2﹣2m﹣3)=﹣m2+2m+8,WK=m+2,
tan∠QKP=![]() =
=![]() =4﹣m=tan∠QPK=
=4﹣m=tan∠QPK=![]() =
=![]() NG,
NG,
则NG=8﹣2m,
MP=AE+![]() GN=
GN=![]() (8﹣2m)=﹣
(8﹣2m)=﹣![]() m+
m+![]() ,
,
KM=KP﹣MP=![]() ,
,
过点F作FL⊥KP于点L,点F(2,1),
则FL=LK=4,则∠LKF=45°,
∵∠MFK=∠PKQ,
tan∠MFK=tan∠QKP=4﹣m,
过点M作MT⊥FK于点T,则KT=MT=![]() (
(![]() ),
),
FT=4![]() ﹣
﹣![]() (
(![]() ),
),
tan∠MFT= =4﹣m,
=4﹣m,
解得:m=11或![]() (舍去11),
(舍去11),
故点Q(![]() ,
,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,将点
,将点![]() 向左平移6个单位长度,得到点
向左平移6个单位长度,得到点![]() .
.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若抛物线![]() 经过点
经过点![]() ,
,![]() ,求抛物线的表达式;
,求抛物线的表达式;
(3)若抛物线![]() 的顶点在直线
的顶点在直线![]() 上移动,当抛物线与线段
上移动,当抛物线与线段![]() 有2个公共点时,求抛物线顶点横坐标
有2个公共点时,求抛物线顶点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为全面贯彻党的教育方针,坚持“健康第一的教育理念,促进学生健康成长,提高体质健康水平,成都市调整体育中考实施方案:分值增加至60,男1000(女80米)必考,足球、篮球、排球“三选一”……从2019年秋季新入学的七年级起开始实施,某1学为了解七年级学生对三大球类运动的喜爱情况,从七年级学生中随机抽取部分学生进行调查问卷,通过分析整理绘制了如下两幅统计图。请根据两幅统计图中的信息回答下列问题:
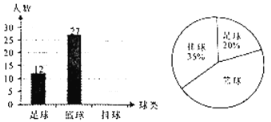
(1)求参与调查的学生中,喜爱排球运动的学生人数,并补全条形图
(2)若该中学七年级共有400名学生,请你估计该中学七年级学生中喜爱篮球运动的学生有多少名?
(3)若从喜爱足球运动的2名男生和2名女生中随机抽取2名学生,确定为该校足球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮两人一起玩投掷一个普通正方体骰子的游戏.
(1)说出游戏中必然事件,不可能事件和随机事件各一个;
(2)如果两个骰子上的点数之积为奇数,小明胜,否则小亮胜,你认为这个游戏公平吗?如果不公平,谁获胜的可能性较大?请说明理由.请你为他们设计一个公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2.
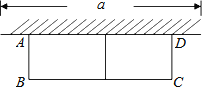
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为45m2的花圃,AB的长是多少米?
(3)当AB的长是多少米时,围成的花圃的面积最大,最大面积为多少m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块长为22 m,宽为17 m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300 m2.若设道路宽为x m,根据题意可列出方程为______________________________.
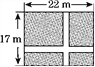
【答案】(22-x)(17-x)=300(或x2-39x+74=0)
【解析】试题分析:把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的草坪是一个长方形,根据长方形的面积公式列方程.设道路的宽应为x米,由题意有(22﹣x)(17﹣x)=300,故答案为:(22﹣x)(17﹣x)=300.
考点:由实际问题抽象出一元二次方程.
【题型】填空题
【结束】
17
【题目】x=1是关于x的一元二次方程x2+mx﹣5=0的一个根,则此方程的另一个根是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③DP2=PHPC;④FE:BC=![]() ,其中正确的个数为( )
,其中正确的个数为( )
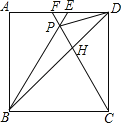
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果公司新购进10000千克柑橘,每千克柑橘的成本为9元. 柑橘在运输、存储过程中会有损坏,销售人员从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录如下:
柑橘总重量n/千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
损坏柑橘重量m/千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.54 |
柑橘损坏的频率 | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
根据以上数据,估计柑橘损坏的概率为 (结果保留小数点后一位);由此可知,去掉损坏的柑橘后,水果公司为了不亏本,完好柑橘每千克的售价至少为________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com