Question

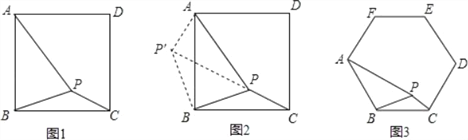
【题目】如图1，在正方形ABCD内有一点P，PA=3，PB=2，PC=1，求∠BPC的度数．

分析：根据已知条件比较分散的特点，我们可以通过旋转变换将分散的已知条件集中在一起，于是将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连结PP′，这时再分别求出∠BP′P和∠AP′P的度数．

解答：（1）请你根据以上分析再通过计算求出图2中∠BPC的度数；

（2）如图3，若在正六边形ABCDEF内有一点P，且PA=2，PB=4，PC=2，求∠BPC的度数．

Answer 1

【答案】（1）135°；（2）120°.

【解析】试题分析：(1)根据旋转的性质得到∠P′BP=90°，BP′=BP=2 ，P′A=PC=1，∠BP′A=∠BPC，则△BPP′为等腰直角三角形，根据等腰直角三角形的性质得PP′= ，PB=2，∠BP′P=45°，利用勾股定理的逆定理可得到△APP′为直角三角形，且∠AP′P=90°，则∠BPC=∠BP′A=45°+90°=135°；（2）把△BPC绕点B逆时针旋转120°，得到了△BP′A，根据旋转的性质得到∠P′BP=120°，BP′=BP=4，P′A=PC=2，∠BP′A=∠BPC，则∠BP′P=∠BPP′=30°，得到P′H=PH，利用含30°的直角三角形三边的关系得到BH= BP′=2，P′H= BH=2 ，得到P′P=2P′H=4，再利用勾股定理的逆定理可得到△APP′为直角三角形，且∠AP′P=90°，于是有∠BPC=∠BP′A=30°+90°=120°.

试题解析：

（1）如图2．

∵△BPC绕点B逆时针旋转90°，得到了△BP′A，

∴∠P′BP=90°，BP′=BP=2 ，P′A=PC=1，∠BP′A=∠BPC，

∴△BPP′为等腰直角三角形，

∴PP′=

PB=2，∠BP′P=45°，

在△APP′中，AP=3

，PP′=2，AP′=1，

∵32=（2）2+12，

∴AP2=PP′2+AP′2，

∴△APP′为直角三角形，且∠AP′P=90°

∴∠BP′A=45°+90°=135°，

∴∠BPC=∠BP′A=135°；

（2）如图3．

∵六边形ABCDEF为正六边形，

∴∠ABC=120°，

把△BPC绕点B逆时针旋转120°，得到了△BP′A，

∴∠P′BP=120°，BP′=BP=4，P′A=PC=2，∠BP′A=∠BPC，

∴∠BP′P=∠BPP′=30°，

过B作BH⊥PP′于H，

∵BP′=BP，

∴P′H=PH，

在Rt△BP′H中，∠BP′H=30°，BP′=4，

∴BH=BP′=2，P′H=BH=2，

∴P′P=2P′H=4，

在△APP′中，AP=2，PP′=4，AP′=2，

∵（2）2=（4）2+22，

∴AP2=PP′2+AP′2，

∴△APP′为直角三角形，且∠AP′P=90°，

∴∠BP′A=30°+90°=120°，

∴∠BPC=120°．