
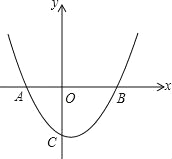
【题目】如图,二次函数图象经过A(﹣3,0)、B(4,0)、C(0,﹣4)三点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴;
(3)该抛物线的对称轴上有一点D,在该抛物线上是否存在一点E,使得以D、E、B、C为顶点的四边形是平行四边形?若存在,求出点E的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣4;(2)x=
x﹣4;(2)x=![]() ;(3)存在,点E的坐标为(
;(3)存在,点E的坐标为(![]() ,﹣
,﹣![]() )、(
)、(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】
试题分析:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),根据点A、B、C的坐标利用待定系数法即可求出抛物线的解析式;(2)根据二次函数的解析式结合二次函数的性质即可得出抛物线的对称轴;(3)假设存在,分线段BC为对角线以及BC为边两种情况考虑,根据点B、C、D的坐标结合平行四边形的性质即可得出点E的坐标,利用二次函数图象上点的坐标特征即可求出点E的坐标,此题得解.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),将A(﹣3,0)、B(4,0)、C(0,﹣4)代入y=ax2+bx+c(a≠0)中得: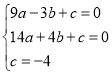 ,解得:
,解得: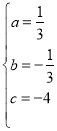 ,∴该抛物线的解析式为y=
,∴该抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣4.(2)∵抛物线的解析式为y=
x﹣4.(2)∵抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣4,∴该抛物线的对称轴为x=﹣
x﹣4,∴该抛物线的对称轴为x=﹣![]() =
=![]() .(3)假设存在,∵点D在抛物线的对称轴上,∴设点D的坐标为(
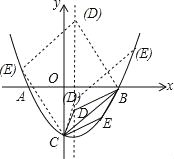
.(3)假设存在,∵点D在抛物线的对称轴上,∴设点D的坐标为(![]() ,m).以D、E、B、C为顶点的四边形是平行四边形分两种情况(如图所示):①当线段BC为对角线时,∵B(4,0)、C(0,﹣4)、D(
,m).以D、E、B、C为顶点的四边形是平行四边形分两种情况(如图所示):①当线段BC为对角线时,∵B(4,0)、C(0,﹣4)、D(![]() ,m),∴点E的坐标为(4﹣
,m),∴点E的坐标为(4﹣![]() , ﹣
, ﹣![]() ,﹣4﹣m),∵点E在抛物线y=
,﹣4﹣m),∵点E在抛物线y=![]() x2﹣
x2﹣![]() x﹣4上,∴﹣4﹣m=
x﹣4上,∴﹣4﹣m=![]() ×
×![]() ﹣
﹣![]() ×
×![]() ﹣4=﹣
﹣4=﹣![]() ,此时点E的坐标为(
,此时点E的坐标为(![]() ,﹣
,﹣![]() );②当线段BC为边时,∵B(4,0)、C(0,﹣4)、D(
);②当线段BC为边时,∵B(4,0)、C(0,﹣4)、D(![]() ,m),∴点E的坐标为(
,m),∴点E的坐标为(![]() +4,m+4)或(
+4,m+4)或(![]() ﹣4,m+4),既(
﹣4,m+4),既(![]() ,m+4)或(﹣
,m+4)或(﹣![]() ,m+4).∵点E在抛物线y=
,m+4).∵点E在抛物线y=![]() x2﹣
x2﹣![]() x﹣4上,∴m+4=
x﹣4上,∴m+4=![]() ×
×![]() ﹣
﹣![]() ×
×![]() ﹣4=
﹣4=![]() 或m+4=
或m+4=![]() ×
×![]() ﹣
﹣![]() ×(﹣
×(﹣![]() )﹣4=
)﹣4=![]() ,此时点E的坐标为(
,此时点E的坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).综上可知:在该抛物线上存在一点E,使得以D、E、B、C为顶点的四边形是平行四边形,点E的坐标为(
).综上可知:在该抛物线上存在一点E,使得以D、E、B、C为顶点的四边形是平行四边形,点E的坐标为(![]() ,﹣
,﹣![]() )、(
)、(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两组同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量![]() (件)与时间
(件)与时间![]() (时)的函数图象如图所示.
(时)的函数图象如图所示.

(1)求甲组加工零件的数量y与时间![]() 之间的函数关系式.
之间的函数关系式.
(2)求乙组加工零件总量![]() 的值.
的值.
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?
查看答案和解析>>
科目:初中数学 来源: 题型:
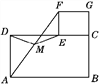
【题目】猜想与证明:如图①摆放矩形纸片ABCD与矩形纸片ECGF,使B,C,G三点在一条直线上,CE在边CD上.连结AF,若M为AF的中点,连结DM,ME,试猜想DM与ME的数量关系,并证明你的结论.
拓展与延伸:
(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为__________________;
(2)如图②摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.[提示:直角三角形斜边上的中线等于斜边的一半]
 ①
① ②
②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系.已知日销售利润=日销售量×一件产品的销售利润.下列结论错误的是( )

A. 第24天的销售量为200件
B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等
D. 第30天的日销售利润是750元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学做了一道数学题:“已知两个多项式为 A、B,B=3x﹣2y,求 A﹣B 的 值.”他误将“A﹣B”看成了“A+B”,结果求出的答案是 x ﹣y,那么原来的 A﹣B的值应该是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊数学家将数:1,3,6,10,15,21,28,…,叫做三角形数,它们有一定的规律性,第24个三角形数与第22个三角形数的差为_________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com