
【题目】如图,在某场足球比赛中,球员甲从球门底部中心点![]() 的正前方
的正前方![]() 处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为
处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为![]() 时达到最高点,此时足球飞行的水平距离为
时达到最高点,此时足球飞行的水平距离为![]() .已知球门的横梁高
.已知球门的横梁高![]() 为
为![]() .
.
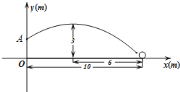
![]() 在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
![]() 守门员乙站在距离球门
守门员乙站在距离球门![]() 处,他跳起时手的最大摸高为
处,他跳起时手的最大摸高为![]() ,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
【答案】(1)能射中球门;(2)他至少后退![]() ,才能阻止球员甲的射门.
,才能阻止球员甲的射门.
【解析】
(1)、根据条件可以得到抛物线的顶点坐标是(4,3),利用待定系数法即可求得函数的解析式;(2)、求出当x=2时,抛物线的函数值,与2.52米进行比较即可判断,再利用y=2.52求出x的值即可得出答案.
(1)、抛物线的顶点坐标是(4,3), 设抛物线的解析式是:y=a(x-4)2+3,
把(10,0)代入得36a+3=0,解得a=-![]() , 则抛物线是y=-
, 则抛物线是y=-![]() (x-4)2+3,
(x-4)2+3,
当x=0时,y=-![]() ×16+3=3-
×16+3=3-![]() =
=![]() <2.44米, 故能射中球门;
<2.44米, 故能射中球门;
(2)当x=2时,y=-![]() (2-4)2+3=
(2-4)2+3=![]() >2.52, ∴守门员乙不能阻止球员甲的此次射门,
>2.52, ∴守门员乙不能阻止球员甲的此次射门,
当y=2.52时,y=-![]() (x-4)2+3=2.52, 解得:x1=1.6,x2=6.4(舍去), ∴2-1.6=0.4(m),
(x-4)2+3=2.52, 解得:x1=1.6,x2=6.4(舍去), ∴2-1.6=0.4(m),
答:他至少后退0.4m,才能阻止球员甲的射门.


科目:初中数学 来源: 题型:
【题目】为了了解某校初三学生每周平均阅读时间的情况,随机抽查了该校初三m名学生,对其每周平均课外阅读时间进行统计,绘制了条形统计图和扇形统计图.
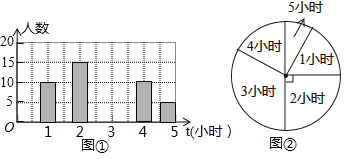
根据以上信息回答下列问题:
(1)求m的值;
(2)求扇形统计图中阅读时间为3小时的扇形圆心角的度数;
(3)求出这组数据的平均数.(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
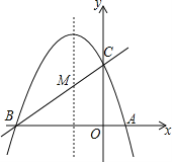
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏果超市用5000元购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨11000元资金购进该种苹果,但这次的进价比试销时每千克多了0.5元,购进苹果的数量是试销时的2倍。
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种的苹果按每千克7元定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?(7分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A1,A2,A3是抛物线y=![]() x2+1(x>0)上的三点,且A1,A2,A3三点的横坐标为连续的整数,连接A1A3,过A2作A2Q⊥x轴于点Q,交A1A3于点P,则线段PA2的长为__.
x2+1(x>0)上的三点,且A1,A2,A3三点的横坐标为连续的整数,连接A1A3,过A2作A2Q⊥x轴于点Q,交A1A3于点P,则线段PA2的长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图(A:0<t≤10,B:10<t≤20,C:20<t≤30,D:t>30),根据图中信息,解答下列问题:
(1)这项被调查的总人数是多少人?
(2)试求表示A组的扇形统计图的圆心角的度数,补全条形统计图;
(3)如果小明想从D组的甲、乙、丙、丁四人中随机选择两人了解平时租用共享单车情况,请用列表或画树状图的方法求出恰好选中甲的概率.
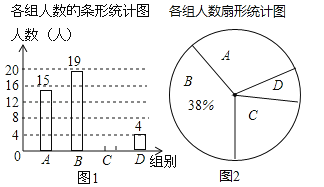
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com