
 如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1.
如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1.分析 (1)利用点平移的坐标规律写出点A1、B1、C1的坐标,然后描点即可得到三角形A1B1C1;
(2)由(1)得到点A1、B1、C1的坐标;
(3)用一个矩形的面积分别减去三个三角形的面积可计算出△ABC的面积.
解答 解:(1)如图,△A1B1C1为所作;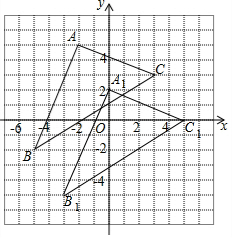
(2)写出点A1、B1、C1的坐标分别为(0,2),(-3,-5),(5,0);
(3)三角形ABC的面积=8×7-$\frac{1}{2}$×2×5-$\frac{1}{2}$×3×7-$\frac{1}{2}$×5×8=$\frac{41}{2}$.
故答案为:(0,2),(-3,-5),(5,0);$\frac{41}{2}$.
点评 本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
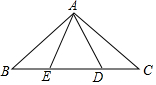 如图,在△ABC中,∠BAC=90°,AB=AC=5,点D,E在BC上,且∠DAE=45°,若CD=$\sqrt{2}$,则DE=$\frac{17\sqrt{2}}{8}$.
如图,在△ABC中,∠BAC=90°,AB=AC=5,点D,E在BC上,且∠DAE=45°,若CD=$\sqrt{2}$,则DE=$\frac{17\sqrt{2}}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单位:min)之间的关系如图所示.
一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单位:min)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
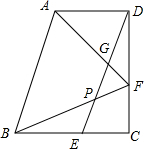 已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=CD,点E、F分别在边BC、CD上,且BE=DF=AD,联结DE,联结AF、BF分别与DE交于点G、P.
已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=CD,点E、F分别在边BC、CD上,且BE=DF=AD,联结DE,联结AF、BF分别与DE交于点G、P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
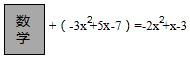
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com