
在等腰梯形ABCD中,AD∥BC,AB=DC,且BC=2.以CD为直径作⊙O1交AD于点E,过点E作EF⊥AB于点F.建立如图所示的平面直角坐标系,已知A、B两点坐标分别为A(2,0)、B(0,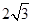 ).
).
1.求C、D两点的坐标;

2.求证:EF为⊙O1的切线
3.线段CD上是否存在点P,使以点P为圆心,PD为半径的⊙P与y轴相切.如果存在,请求出P点坐标;如果不存在,请说明理由.
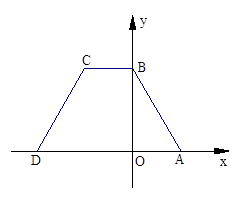
1.连结CE

∵CD是⊙O1的直径 ∴CE⊥x轴
∴在等腰梯形ABCD中,EO=BC=2,
CE=BO= ,DE=AO=2∴DO=4,
,DE=AO=2∴DO=4,
故C(![]() )D(
)D(![]() ) (3分)
) (3分)
2.连结O1E,在⊙O1中,O1D= O1E,∠O1DE=∠1,

又在等腰梯形ABCD中 ∠CDA=∠BAD
∴∠1=∠BAD ∴O1E∥BA
又∵EF⊥BA ∴O1E⊥EF
∵E在⊙O1上 ∴EF为⊙O1的切线. (6分)
3.存在满足条件的点P.
作PH⊥OD于H,作PM⊥y轴于M.
则当PM=PD时,⊙P于y轴相切.
在矩形PHOM中,OH=PM
设OH=m, 则PM=PD=m, DH=4-m
∵tan∠OAB=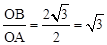
∴∠OAB=60°
∴∠PDH=∠OAB=60°
在Rt△PDH中,cos∠PDH=![]() ,即:
,即:![]() , m=
, m=![]() ,
,
则PH=DH·tan∠PDH=(4-m) ![]()
∴ 满足条件的P点坐标为(![]() ) (12分)
) (12分)
解析:(1)连CE,根据圆周角定理的推论得到CE⊥DE,再根据等腰梯形的性质得DE=OA=2,则OD=2+2=4,即可写出C点坐标和D点坐标;
(2)AB=4,易得∠DCE=30°,则∠CDE=∠A=60°,得到△O1DE为等边三角形,则∠O1ED=60°,而EF⊥AB,有∠FEA=30°,于是∠O1EF=90°,根据切线的判定即可得到结论;
(3)设⊙与y轴相切于F,连PF,过C作CE⊥x轴与E,交PF于H,⊙P的半径为R,根据切线的性质得PF⊥y轴,则PD=PF=R,所以有PH=R-2,PC=4-R,DE=2,易证得Rt△CPH∽Rt△GDF,理由相似比可求出R和CH,可得到HE,即可写出P点坐标.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且查看答案和解析>>
科目:初中数学 来源: 题型:
 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.查看答案和解析>>
科目:初中数学 来源: 题型:
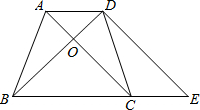 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com