
���� ��1���ⲻ��ʽ������������⣬���ݹ������̵Ķ���д��һ����Ϊ2�ķ��̼��ɣ�
��2���������������x��ֵ���Ӷ�ȷ������ʽ��������⼴�ɵó�m�ķ�Χ��
��� �⣺��1���ⲻ��ʽx-$\frac{1}{2}$��2���ã�x��2.5��
�ⲻ��ʽ1+x��-3x+6���ã�x��1.25��
��ʽ��Ľ⼯Ϊ1.25��x��2.5��
����������Ϊ2��
��ò���ʽ��Ĺ�������Ϊx-2=0��
�ʴ�Ϊ��x-2=0��
��2���ⷽ��3-x=2x��x=1��
�ⷽ��3+x=2��x+$\frac{1}{2}$����x=2��
�ⲻ��ʽ��$\left\{\begin{array}{l}x��2x-m\\ x-2��m\end{array}\right.$��m��x��m+2��
��1��2���Ǹò���ʽ��Ľ⣬
��0��m��1��
���� ������Ҫ�����һԪһ�η��̺�һԪһ�β���ʽ�飬�������ս�һԪһ�η��̺�һԪһ�β���ʽ��ļ����ǽ���Ĺؼ���


 ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
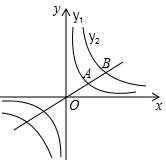 ��ͼ����ԭ��O��ֱ���뷴��������y1��y2��ͼ���ڵ�һ�����ڷֱ��ڵ�A��B����AΪOB���е㣮����B������Ϊ��8��2������y1��x�ĺ�������ʽ��y1=$\frac{4}{x}$��
��ͼ����ԭ��O��ֱ���뷴��������y1��y2��ͼ���ڵ�һ�����ڷֱ��ڵ�A��B����AΪOB���е㣮����B������Ϊ��8��2������y1��x�ĺ�������ʽ��y1=$\frac{4}{x}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
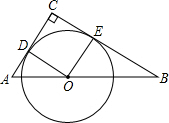 ��ͼ���ڡ�ABC�У���C=90�㣬��O��б��AB��һ�㣬��OΪԲ�ĵġ�O�ֱ����AC��BC�����ڵ�D��E������OD��OE��
��ͼ���ڡ�ABC�У���C=90�㣬��O��б��AB��һ�㣬��OΪԲ�ĵġ�O�ֱ����AC��BC�����ڵ�D��E������OD��OE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com