
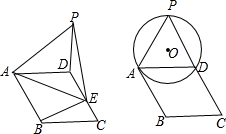
 已知:如图?ABCD中,CD=CB=3,∠C=60°,点E是CD边上自C向D的动点(点E到点D停止运动),连结AE,以AE为边作等边△AEP,连结DP.
已知:如图?ABCD中,CD=CB=3,∠C=60°,点E是CD边上自C向D的动点(点E到点D停止运动),连结AE,以AE为边作等边△AEP,连结DP.分析 (1)首先证明∠PAD=∠BAE,则根据SAS即可证明两个三角形全等;
(2)根据△ADP是等边三角形,则O是三角形ADP的中心,即可求得∠DAO=30°,从而证明∠BAO=90°,则AB与⊙O相切;
(3)在运动过程中,始终保持△ABE≌△ADP,则点P的运动路径长等于E点运动的路径长,据此即可求解.
解答 (1)证明:∵?ABCD中,CD=CB,
∴四边形ABCD是菱形,
∴AD=AB,∠C=∠BAD=60°.
∵△AEP是等边三角形,
∴AP=AE,∠PAE=60°,
∴∠PAD=∠BAE,
∴△ABE和△ADP中,
$\left\{\begin{array}{l}{AP=AE}\\{∠PAD=∠EAB}\\{AD=AB}\end{array}\right.$,
∴△ABE≌△ADP;
(2)解:直线AB于⊙O相切.
连接OA,
∵△PAD是等边三角形,
∴∠DAO=30°,
∴∠BAO=∠DAO+∠DAB=90°,
又∵A在⊙O上,
∴AB与⊙O相切;
(3)解:∵在运动过程中,始终保持△ABE≌△ADP,
∴点P的运动路径长=CD=3.
故答案是:3.
点评 本题考查了全等三角形的判定与性质,正确证明∠PAD=∠BAE是解决本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
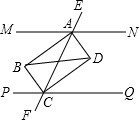 已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{11}{3}$ | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
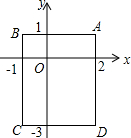 如图,在平面直角坐标系xoy中,已知点A(2,1)、B(-1,1)、C(-1,-3)、D(2,-3),把一根长为2015个单位长度没有弹性的细线(线的粗细忽略不计)的一端固定在D处,并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标为(2,-2).
如图,在平面直角坐标系xoy中,已知点A(2,1)、B(-1,1)、C(-1,-3)、D(2,-3),把一根长为2015个单位长度没有弹性的细线(线的粗细忽略不计)的一端固定在D处,并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标为(2,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
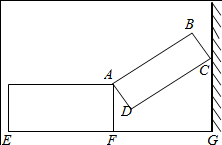 如图,一种侧面形状为矩形的行李箱,箱盖打开后,盖子的一端靠在墙上,此时BC=10cm,箱底端点E与墙角G的距离为65cm,∠DCG=60°.
如图,一种侧面形状为矩形的行李箱,箱盖打开后,盖子的一端靠在墙上,此时BC=10cm,箱底端点E与墙角G的距离为65cm,∠DCG=60°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
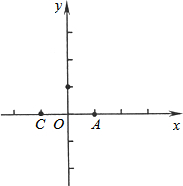 在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去.则点P3的坐标为(0,-2);点Pn在y轴上,则点Pn的坐标为(0,0)或(0,-2).
在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去.则点P3的坐标为(0,-2);点Pn在y轴上,则点Pn的坐标为(0,0)或(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
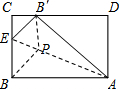 如图所示,矩形纸片ABCD中,AB=5,AD=4,将纸片折叠,使点D落在边CB上的D′处,折痕为AE,在折痕AE上存在一点P到边CB的距离与到点D的距离相等,则此相等距离为2.5.
如图所示,矩形纸片ABCD中,AB=5,AD=4,将纸片折叠,使点D落在边CB上的D′处,折痕为AE,在折痕AE上存在一点P到边CB的距离与到点D的距离相等,则此相等距离为2.5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,∠BAD的平分线交BC的延长线于点E,交CD于点G,过点E作EF∥CD,过点G作FG∥EC,EF,FG交于点F.求证:四边形CEFG为菱形.
如图,在平行四边形ABCD中,∠BAD的平分线交BC的延长线于点E,交CD于点G,过点E作EF∥CD,过点G作FG∥EC,EF,FG交于点F.求证:四边形CEFG为菱形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com