公式介绍: 1+2+3+4+5+-+n＝? 将另外1+2+3+4+5+-+n＝?与原来n+(n-1)+-+3+2+1排在一起.拼成一个长为(n+1)宽为n的矩形.总数为n+(n+1)个．所以可得1+2+3+4+5+-+n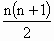＝．请你计算:①1+2+3+4+-+2001+2002＝ , ②1000+1001+1002+-2001+2002＝．题目和参考答案——青夏教育精英家教网—

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

科目：初中数学 来源： 题型：

小王到玻璃店选购一块镶边框的矩形镜子，要求宽与长之比为1：2．售货员介绍镜子价格计算公式为：镜子总价（元）=镜面面积（平方米）×单价（a元/平方米）+边框长度（米）×单价（b元/米）+加工费（20元/块）．（边框宽度忽略不计）
（1）写出镜子的总价y（元）与矩形镜面宽x（米）之间的关系式（用含a、b的式子表示，不要求写出自变量取值范围）．
（2）售货员为小王计算了两种规格镜子的价格：①宽0.5米×长1米，总价为110元；②宽1米×长2米，总价为320元，请求出a和b的值．
（3）小王花了200元买回一块镜子，请你求出他购买的镜子的规格．

查看答案和解析>>

科目：初中数学 来源： 题型：阅读理解

仔细阅读以下内容解决问题：
偏微分方程，对于多个变量的求最值问题相当有用，以2001年全国联赛第二试第一题为例给同学们作一介绍，问题建立数学模型后实际上是求：
y=5a²+6ab+3b²-30a-20b+46的最小值，先介绍求导公式，（xⁿ）′=nx^n-1，a′=0（a为常数），当y_a′=10a+6b-30=0，y_b′=6a+6b-20=0时，可取得最小值（y_a′的意思是关于a求导，把b看作常数，（5a²）′=10a，（6ab）′=6b，（3a²-20b+46）′=0）．解方程，得a=

5

2

，b=

5

6

，代入可得y=

1

6

，即是最小值．
同学们：以上内容很有挑战性，确保读懂后请解答下面问题：运用阅读材料中的知识求s=4x²+2y²+4xy-12x-8y+17的最小值

7

．

查看答案和解析>>

科目：初中数学 来源：2011年浙江省一级重点中学自主招生考试数学仿真试卷（七）（解析版） 题型：填空题

仔细阅读以下内容解决问题：
偏微分方程，对于多个变量的求最值问题相当有用，以2001年全国联赛第二试第一题为例给同学们作一介绍，问题建立数学模型后实际上是求：
y=5a²+6ab+3b²-30a-20b+46的最小值，先介绍求导公式，（xⁿ）′=nx^n-1，a′=0（a为常数），当y_a′=10a+6b-30=0，y_b′=6a+6b-20=0时，可取得最小值（y_a′的意思是关于a求导，把b看作常数，（5a²）′=10a，（6ab）′=6b，（3a²-20b+46）′=0）．解方程，得a=

，b=

，代入可得y=

，即是最小值．
同学们：以上内容很有挑战性，确保读懂后请解答下面问题：运用阅读材料中的知识求s=4x²+2y²+4xy-12x-8y+17的最小值．

查看答案和解析>>

科目：初中数学 来源：2011年安徽省合肥市包河区中考数学二模试卷（解析版） 题型：解答题

小王到玻璃店选购一块镶边框的矩形镜子，要求宽与长之比为1：2．售货员介绍镜子价格计算公式为：镜子总价（元）=镜面面积（平方米）×单价（a元/平方米）+边框长度（米）×单价（b元/米）+加工费（20元/块）．（边框宽度忽略不计）
（1）写出镜子的总价y（元）与矩形镜面宽x（米）之间的关系式（用含a、b的式子表示，不要求写出自变量取值范围）．
（2）售货员为小王计算了两种规格镜子的价格：①宽0.5米×长1米，总价为110元；②宽1米×长2米，总价为320元，请求出a和b的值．
（3）小王花了200元买回一块镜子，请你求出他购买的镜子的规格．

查看答案和解析>>

练习册

高中

初中

小学