
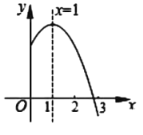
【题目】已知二次函数![]() (
(![]() 是常数,
是常数,![]() )图象的对称轴是直线
)图象的对称轴是直线![]() ,其图象的一部分如图所示,下列说法中①
,其图象的一部分如图所示,下列说法中①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④
;④![]() ;⑤
;⑤![]() .正确的结论有( )
.正确的结论有( )
A.①②④B.②③④C.①③⑤D.①②③④⑤
【答案】A
【解析】
由抛物线的开口方向判断a,由抛物线与y轴的交点判断c,根据对称轴的位置判断b及a、b关系,从而判断①②,根据抛物线与x轴交点情况可判断③④,由y=ab+c<0结合![]() 即可判断⑤.
即可判断⑤.
解:抛物线开口向下,则a<0.对称轴在y轴右侧,a、b异号,则b>0.抛物线与y轴交于正半轴,则c>0,所以abc<0,故①正确;
∵抛物线的对称轴是直线x=1,
则![]() ,即b=-2a,
,即b=-2a,
∴![]() ,故②正确;
,故②正确;
由图象可知,抛物线与x轴的左交点位于0和1之间,在两个交点之间时,y>0,在x=3和x=1时,y<0,故③错误;
∵当x=1时,有y=ab+c<0,故④正确;
∵![]() ,
,
∴a=![]() ,
,
∵ab+c<0,
∴![]() ,即
,即![]() ,
,
整理得![]() ,故⑤错误,
,故⑤错误,
∴正确的有①②④,
故选:A.


科目:初中数学 来源: 题型:
【题目】2018年国务院机构改革不再保留国家卫生和计划生育委员会,组建国家卫生健康委员会,在修正人口普查数据中的低龄人口漏登后,我们估计了1982-2030年育龄妇女情况.1982年中国15-49岁育龄妇女规模为2.5亿,到2011年达3.8亿人的峰值,2017年降至3.5亿,预计到2030年将降至3.0亿.则数据2.5亿、3.8亿、3.5亿、3.0亿的中位数、平均数、方差分别是( )
A.3.25亿、3.2亿、0.245B.3.65亿、3.2亿、0.98
C.3.25亿、3.2亿、0.98D.3.65亿、3亿、0.245
查看答案和解析>>
科目:初中数学 来源: 题型:
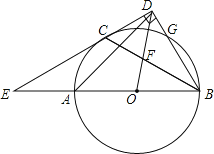
【题目】如图:AB是⊙O的直径,C、G是⊙O上两点,且点C是劣弧AG的中点,过点C的直线CD⊥BG的延长线于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线;
(2)若ED=![]() DB,求证:3OF=2DF;
DB,求证:3OF=2DF;
(3)在(2)的条件下,连接AD,若CD=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
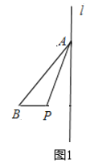
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 垂直于线段
垂直于线段![]() 所在的直线.设点
所在的直线.设点![]() ,
,![]() 关于直线
关于直线![]() 的对称点分别为点
的对称点分别为点![]() ,
,![]()
(1)在图1中画出![]() 关于直线
关于直线![]() 对称的三角形
对称的三角形![]() .
.
(2)若![]() ,求
,求![]() 的度数.(用
的度数.(用![]() 表示)
表示)
(3)若点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,
,![]() .请写出
.请写出![]() 、
、![]() 之间的数量关系和位置关系,并证明你的结论.
之间的数量关系和位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
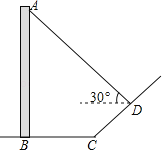
【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
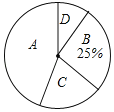
【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调査(问卷调査表如图所示),将调査结果整理后绘制例图1、图2两幅均不完整的统计图表.
最受欢迎的校本课程调查问卷
您好!这是一份关于您最喜欢的校本课程问卷调查表,请在表格中选择一个(只能选一个)您最喜欢的课程选项,在其后空格内打“√”,非常感谢您的合作.
选项 | 校本课程 | |
A | 3D打印 | |
B | 数学史 | |
C | 诗歌欣赏 | |
D | 陶艺制作 |
校本课程 | 频数 | 频率 |
A | 36 | 0.45 |
B | 0.25 | |
C | 16 | b |
D | 8 | |
合计 | a | 1 |
请您根据图表中提供的信息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调査结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
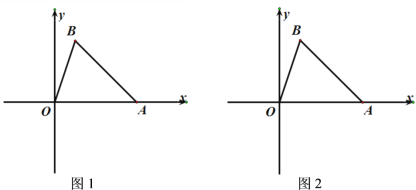
【题目】在平面直角坐标系xoy中,已知 A(4,0)、B(1,3), 过![]() 的直线
的直线![]() 是绕着△OAB的顶点A旋转,与y轴相交于点P,探究解决下列问题:
是绕着△OAB的顶点A旋转,与y轴相交于点P,探究解决下列问题:
(1)如图1所示,当直线![]() 旋转到与边OB相交时,试用无刻度的直尺和圆规确定点P的位置,使顶点O、B到直线
旋转到与边OB相交时,试用无刻度的直尺和圆规确定点P的位置,使顶点O、B到直线![]() 的距离之和最大,(保留作图痕迹);
的距离之和最大,(保留作图痕迹);
(2)当直线![]() 旋转到与y轴的负半轴相交时,使顶点O、B到直线
旋转到与y轴的负半轴相交时,使顶点O、B到直线![]() 的距离之和最大,请直接写出点P的坐标是 .(可在图2中分析)
的距离之和最大,请直接写出点P的坐标是 .(可在图2中分析)
查看答案和解析>>
科目:初中数学 来源: 题型:
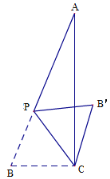
【题目】如图,在△ABC 中,∠ACB=90°,AC=12,BC=5,P 是边 AB 上的动点(不与点 B 重合),将△BCP 沿 CP 所在的直线翻折,得到△B'CP,连接 B'A,B'A 长度的最小值是 m,B'A 长度的最大值是 n,则 m+n 的值等于 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】装商店销售![]() 台
台![]() 型和
型和![]() 台
台![]() 型电脑的利润为
型电脑的利润为![]() 元,销售
元,销售![]() 台
台![]() 型和
型和![]() 台,
台, ![]() 型电脑的利润为
型电脑的利润为![]() 元.
元.
(1)求每台![]() 型电脑和
型电脑和![]() 型电脑的销售利润;
型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共 ![]() 台,其中
台,其中![]() 型电脑的进货量不超过
型电脑的进货量不超过![]() 型电脑的
型电脑的![]() 倍,购进
倍,购进![]() 型电脑
型电脑![]() 台,这
台,这![]() 台电脑的销售总利润为
台电脑的销售总利润为![]() 元.间该商店购进
元.间该商店购进![]() 型
型![]() 服各多少台.才能使销售利润
服各多少台.才能使销售利润![]() 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com