
【题目】已知,点P是直角三角形ABC斜边AB上一点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.

(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系是 ;
(2)如图2,当点P在线段AB上不与点Q重合时,若AC=BC,CE:AE=1:3,△FBQ的面积等于3,求△AQE的面积;
(3)如图3,当点P在线段BA的延长线上时,请画出符合条件的图形.若AC=BC,AE:CE=1:3,△FEQ的面积等于3,求△AQE的面积.
【答案】(1)AE∥BF,QE=QF;(2)9;(3)![]() .
.
【解析】
(1)根据AAS推出△AEQ≌△BFQ,推出AE=BF即可;(2)延长EQ交BF于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EA=BD,再证明△AEQ≌△BDQ,所以AE=BD,CE=BF,又因为CE:AE=1:3,从而得BF:BD=1:3,即△FBQ的面积:△DBQ的面积=1:3,计算△DBQ的面积=9,从而求解;(3)方法同(2)证出 Rt△AEC≌Rt△CFB,连接CQ, 由AE:CE=1:3,得CF:CE=1:3,再根据高相等的三角形面积比等于底的比得出△CFQ的面积与△EFQ的面积面积比,从而求出△CFQ的面积,然后根据SAS 证明 △QAE≌△QCF,从而求解.
解:(1)当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是AE=BF,
理由是:∵Q为AB的中点,
∴AQ=BQ,
∵AE⊥CQ,BF⊥CQ,
∴AE∥BF,∠AEQ=∠BFQ=90°,
在△AEQ和△BFQ中,
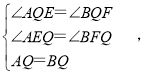
∴△AEQ≌△BFQ,
∴QE=QF,
故答案为:AE∥BF,QE=QF;
(2) 延长EQ交BF于D,如图2: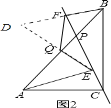
∵由(1)知:AE∥BF,
∴∠AEQ=∠BDQ,
在△AEQ和△BDQ中,
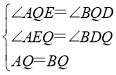
∴△AEQ≌△BDQ,
∴AE=BD,
∵∠ACE+∠FCB=∠FCB+∠CBF=90°
∴∠ACE =∠CBF
又∵∠AEC=∠CFB=90°,AC=CB,
∴△AEQ≌△BDQ
∴AE=BD,CE=BF
又∵CE:AE=1:3,∴BF:BD=1:3,即△FBQ的面积:△DBQ的面积=1:3
又∵△FBQ的面积等于3,∴△DBQ的面积=9,
∵△AEQ≌△BDQ,
∴△AEQ的面积=9;
(3)图形如下:连接CQ,
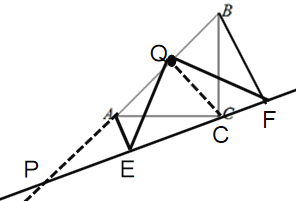
方法同(2)可得:Rt△AEC≌Rt△CFB(一线三等角),
∴AE=CF,EC=FB,∠EAC=∠FCB,
∵AE:CE=1:3,
∴CF:CE=1:3,
∴△CFQ的面积:△ECQ的面积=1:3,△CFQ的面积:△EFQ的面积=1:4,△FEQ的面积等于3,
即:△CFQ的面积=![]() ,
,
∵Q为斜边AB的中点,AC=BC,
∴CQ=AQ,∠QAC=∠QCB=45°,
∴∠EAC+∠QAC =∠FCB+∠QCB,
即∠QAE=∠QCF
∴△QAE≌△QCF (SAS)
∴△AQE的面积=△CFQ的面积=![]() ,
,


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】把1,2,3,4......按下列方式排列:
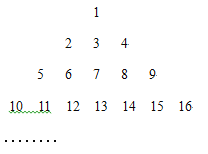
(1)按照这样的排列,第8行的最后一个数是 ,这个数的平方根是 ;正中间一列,自上而下第![]() 个数是 (用
个数是 (用![]() 表示);
表示);
(2)求第15行所有数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
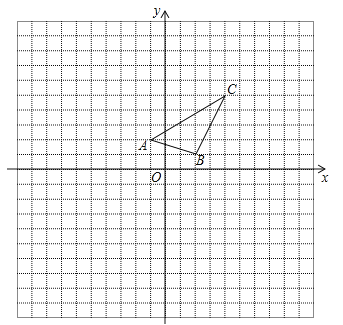
【题目】如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
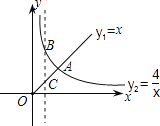
【题目】函数y1=x(x≥0),y2=![]() (x>0)的图象如图6-Z-6所示,则下列结论:
(x>0)的图象如图6-Z-6所示,则下列结论:
①两函数图象的交点A的坐标为(2,2);
②当x>2时,y1>y2;
③当x=1时,BC=3;
④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.
其中正确结论的序号是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了治理大气污染,我国西部某市抽取了该市2019年中120天的空气质量指数,绘制了如下不完整的统计图表:

(1) ![]() ;
;![]() .
.
(2)请把空气质量指数的条形统计图补充完整;
(3)若绘制“空气质量指数的扇形统计图”,级别为“优”所对应扇形的圆心角的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1.
![]()
(1)如果点A,D表示的数互为相反数,那么点B表示的数是多少?
(2)如果点B,D表示的数互为相反数,那么图中表示的四个点中,哪一点表示的数的绝对值最大?为什么?
(3)当点B为原点时,若存在一点M到A的距离是点M到D的距离的2倍,则点M所表示的数是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图 1,已知点 F,G 分别在直线 AB,CD 上,且 AB∥CD,若∠BFE=40°,∠CGE=130°,则∠GEF 的度数为 ;
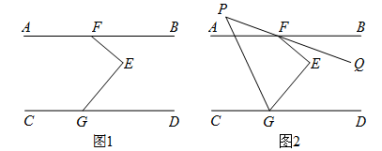
(2)拓展探究:∠GEF,∠BFE,∠CGE 之间有怎样的数量关系?写出结论并给出证明; 答:∠GEF= .
证明:过点 E 作 EH∥AB,
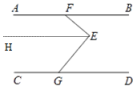
∴∠FEH=∠BFE( ),
∵AB∥CD,EH∥AB,(辅助线的作法)
∴EH∥CD( ),
∴∠HEG=180°-∠CGE( ),
∴∠FEG=∠HFG+∠FEH= .
(3)深入探究:如图 2,∠BFE 的平分线 FQ 所在直线与∠CGE 的平分线相交于点 P,试探究∠GPQ 与∠GEF 之间的数量关系,请直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,b)、点B(a,0)、点D(d,0)且a、b、c满足![]() .DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
.DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
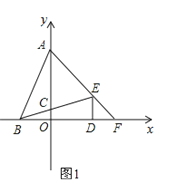
(1)求点A、B、D的坐标;
(2)求点C、E、F的坐标;
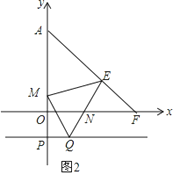
(3)如图,过P(0,-1)作x轴的平行线,在该平行线上有一点Q(点Q在P的右侧)使∠QEM=45°,QE交x轴于N,ME交y轴正半轴于M,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com