
 如图,观察每一个图中黑色正六边形的排列规律,第10个图中黑色正六边形有100个,第n个图中黑色正六边形有n2个.
如图,观察每一个图中黑色正六边形的排列规律,第10个图中黑色正六边形有100个,第n个图中黑色正六边形有n2个. 分析 从图案分析可知,第1个图中黑色正六边形的个数都是1的平方,第2个图中黑色正六边形的个数都是2的平方,第3个图中黑色正六边形的个数都是3的平方,依此类推可得规律:第n个图中黑色正六边形有n2个,那么第10个图中黑色正六边形个数可求.
解答 解:第1个图中黑色正六边形的个数是:12=1,
第2个图中黑色正六边形的个数是:22=4,
第3个图中黑色正六边形的个数是:32=9,
…
第n个图中黑色正六边形有n2个.
第10个图中黑色正六边形的个数是:102=100.
故答案为:100,n2.
点评 本题主要考查图形的变化规律,首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
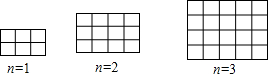
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等腰直角△ABC中,∠ACB=90°,点D在BA的延长线上,连接CD,过点C作CE⊥CD,使CE=CD,连接BE,若点N为BD的中点,连接CN、BE.
如图,等腰直角△ABC中,∠ACB=90°,点D在BA的延长线上,连接CD,过点C作CE⊥CD,使CE=CD,连接BE,若点N为BD的中点,连接CN、BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
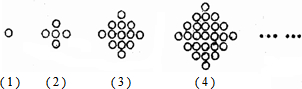
| A. | 145个 | B. | 162 | C. | 181个 | D. | 202个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
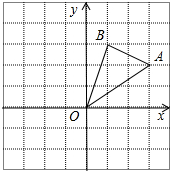 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O顺时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O顺时针旋转90°后得到△A1OB1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 花钱数额(元) | 5 | 10 | 15 | 20 | 25 |
| 学生人数 | 7 | 12 | 18 | 10 | 3 |
| A. | 15,15 | B. | 18,15 | C. | 25,18 | D. | 15,18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com