
分析 因为x、y为指数,我们目前无法求出x、y的值,而$\frac{1}{x}+\frac{1}{y}=\frac{y+x}{xy}$,其实只需求出x+y、xy的值或它们的关系,自然想到指数运算律.
解答 解:由已知得$200{0}^{\frac{1}{x}}$=80,$200{0}^{\frac{1}{y}}$=25,
两式相乘,得$200{0}^{\frac{1}{x}}$×$200{0}^{\frac{1}{y}}$=$200{0}^{\frac{1}{x}+\frac{1}{y}}$=25×80=20001,
所以$\frac{1}{x}+\frac{1}{y}$=1.
点评 本题考查了同底数幂的乘法运算法则,将已知条件转化为分数指数是解题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{x+1}$ | B. | $\root{3}{{x}^{3}+1}$ | C. | $\root{3}{x}$+1 | D. | x+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
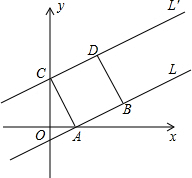 在平面直角坐标中,A为x轴上一点,过A点的直线L的解析式为y=kx-k(其中k为常数,且k≠0),B(3,m)为直线L上的另一点,C是y轴上一动点,过C点作直线L的平行线L′,连结AC,过B点作BD∥AC交于L′于D点.
在平面直角坐标中,A为x轴上一点,过A点的直线L的解析式为y=kx-k(其中k为常数,且k≠0),B(3,m)为直线L上的另一点,C是y轴上一动点,过C点作直线L的平行线L′,连结AC,过B点作BD∥AC交于L′于D点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com