
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy![]() гыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЎ
гыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉХаЖЯЁїABCЕФаЮзДЃЛ
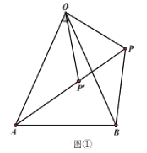
ЃЈ2ЃЉЙ§ЕуCЕФжБЯпy![]() НЛxжсгкЕуHЃЌШєЕуPЪЧЕкЫФЯѓЯоФкХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЧвдкЖдГЦжсЕФгвВрЃЌЙ§ЕуPзїPQЁЮyжсНЛжБЯпCHгкЕуQЃЌзїPNЁЮxжсНЛЖдГЦжсгкЕуNЃЌвдPQЁЂPNЮЊСкБпзїОиаЮPQMNЃЌЕБОиаЮPQMNЕФжмГЄзюДѓЪБЃЌдкyжсЩЯгавЛЖЏЕуKЃЌxжсЩЯгавЛЖЏЕуTЃЌвЛЖЏЕуGДгЯпЖЮCPЕФжаЕуRГіЗЂвдУПУы1ИіЕЅЮЛЕФЫйЖШбиRЁњKЁњTЕФТЗОЖдЫЖЏЕНЕуTЃЌдйбиЯпЖЮTBвдУПУы2ИіЕЅЮЛЕФЫйЖШдЫЖЏЕНBЕуДІЭЃжЙдЫЖЏЃЌЧѓЖЏЕуGдЫЖЏЕФзюЩйЪБМфМАДЫЪБЕуTЕФзјБъЃЛ
НЛxжсгкЕуHЃЌШєЕуPЪЧЕкЫФЯѓЯоФкХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЧвдкЖдГЦжсЕФгвВрЃЌЙ§ЕуPзїPQЁЮyжсНЛжБЯпCHгкЕуQЃЌзїPNЁЮxжсНЛЖдГЦжсгкЕуNЃЌвдPQЁЂPNЮЊСкБпзїОиаЮPQMNЃЌЕБОиаЮPQMNЕФжмГЄзюДѓЪБЃЌдкyжсЩЯгавЛЖЏЕуKЃЌxжсЩЯгавЛЖЏЕуTЃЌвЛЖЏЕуGДгЯпЖЮCPЕФжаЕуRГіЗЂвдУПУы1ИіЕЅЮЛЕФЫйЖШбиRЁњKЁњTЕФТЗОЖдЫЖЏЕНЕуTЃЌдйбиЯпЖЮTBвдУПУы2ИіЕЅЮЛЕФЫйЖШдЫЖЏЕНBЕуДІЭЃжЙдЫЖЏЃЌЧѓЖЏЕуGдЫЖЏЕФзюЩйЪБМфМАДЫЪБЕуTЕФзјБъЃЛ
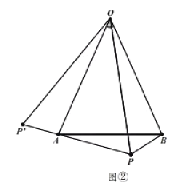
ЃЈ3ЃЉШчЭМ2ЃЌНЋЁїABCШЦЕуBЫГЪБеыа§зЊжСЁїA'BC'ЕФЮЛжУЃЌЕуAЁЂCЕФЖдгІЕуЗжБ№ЮЊA'ЁЂC'ЃЌЧвЕуC'ЧЁКУТфдкХзЮяЯпЕФЖдГЦжсЩЯЃЌСЌНгAC'ЃЎЕуEЪЧyжсЩЯЕФвЛИіЖЏЕуЃЌСЌНгAEЁЂC'EЃЌНЋЁїAC'EбижБЯпC'EЗелЮЊЁїAЁхC'EЃЌЪЧЗёДцдкЕуA'ЃЌЪЙЕУЁїBAAЁхЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕуEЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
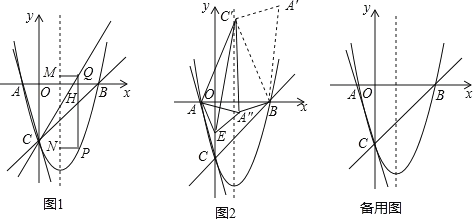
ЁОД№АИЁПЃЈ1ЃЉЁїABCЪЧвдACЮЊЕзЕФЕШбќШ§НЧаЮЃЎРэгЩМћНтЮіЃЛЃЈ2ЃЉЖЏЕуGдЫЖЏЕФзюЩйЪБМфt=6![]() УыЃЌTЃЈ
УыЃЌTЃЈ![]() ЃЌ0ЃЉЃЛЃЈ3ЃЉEзјБъЮЊЃЈ0ЃЌ3
ЃЌ0ЃЉЃЛЃЈ3ЃЉEзјБъЮЊЃЈ0ЃЌ3![]() ЃЉЛђЃЈ0ЃЌ6ЃЉЛђЃЈ0ЃЌ3
ЃЉЛђЃЈ0ЃЌ6ЃЉЛђЃЈ0ЃЌ3![]() ЃЉЛђЃЈ0ЃЌ12ЃЉЃЎ
ЃЉЛђЃЈ0ЃЌ12ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНсТлЃКЁїABCЪЧвдACЮЊЕзЕФЕШбќШ§НЧаЮЃЌЧѓГіAЃЌBЃЌCЕФзјБъЃЌЧѓГіBCЃЌBAМДПЩХаЖЯЃЎ
ЃЈ2ЃЉИљОнжмГЄЕФЖЈвхЃЌЙЙНЈЖўДЮКЏЪ§ЃЌЧѓГіжмГЄзюДѓЪБЃЌЕуPЃЈ3![]() ЃЌ-3
ЃЌ-3![]() ЃЉЃЌвђЮЊRЮЊЯпЖЮCPЕФжаЕуЃЌЭЦГіRЃЈ
ЃЉЃЌвђЮЊRЮЊЯпЖЮCPЕФжаЕуЃЌЭЦГіRЃЈ![]() ЃЌ-3
ЃЌ-3![]() ЃЉЃЌзїЕуRЙигкyжсЖдГЦЕуRЁфЃЈ
ЃЉЃЌзїЕуRЙигкyжсЖдГЦЕуRЁфЃЈ![]() ЃЌ-3
ЃЌ-3![]() ЃЉЃЌДЫЪБRгыNжиКЯЃЌгЩЬтвтжЊЃКЖЏЕуGдЫЖЏЕФзюЩйЪБМфt=RK+KT+
ЃЉЃЌДЫЪБRгыNжиКЯЃЌгЩЬтвтжЊЃКЖЏЕуGдЫЖЏЕФзюЩйЪБМфt=RK+KT+![]() TBЃЌЙ§ЕуRЁфзїRЁфJЁЭBSгкJЃЌНЛyжсгкKЃЌНЛxжсгкTЃЌдђRЁфJМДЮЊЫљЧѓЃЌгЩTJ=
TBЃЌЙ§ЕуRЁфзїRЁфJЁЭBSгкJЃЌНЛyжсгкKЃЌНЛxжсгкTЃЌдђRЁфJМДЮЊЫљЧѓЃЌгЩTJ=![]() TBЃЌПЩЕУt=RЁфK+KT+TJЃЌдйРћгУЯрЫЦШ§НЧаЮЕФаджЪЧѓГіTMМДПЩНтОіЮЪЬтЃЎ
TBЃЌПЩЕУt=RЁфK+KT+TJЃЌдйРћгУЯрЫЦШ§НЧаЮЕФаджЪЧѓГіTMМДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉЗжЫФжжЧщаЮЗжБ№ЛГіЭМаЮЧѓНтМДПЩЃКЂйЕБAA'=A'BЪБЃЌШчЭМ2жаЃЎЂкЕБAA'=ABЪБЃЌШчЭМ3жаЃЌЩшAЁхCЁфНЛyжсгкJЃЎЂлЕБAA'=A'BЪБЃЌШчЭМ4жаЃЌЩшACЁфНЛyжсгкMЃЎЂмЕБA'B=ABЪБЃЌШчЭМ5жаЃЎЗжБ№ЧѓГіД№АИМДПЩ.
НтЃКЃЈ1ЃЉЁїABCЪЧвдACЮЊЕзЕФЕШбќШ§НЧаЮЃЎРэгЩШчЯТЃК
гЩЬтвтжЊХзЮяЯпy![]() гыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌ
гыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌ
ЁрСюx=0ЃЌНтЕУЃКy![]() ЃЛСюx=0ЃЌНтЕУЃКx1
ЃЛСюx=0ЃЌНтЕУЃКx1![]() ЃЌx2=4
ЃЌx2=4![]() ЃЛ
ЃЛ
ЁрAЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЁрAC2=AM2+MC2![]() 30ЃЌ
30ЃЌ
BC2=OB2+OC2![]() 75ЃЌ
75ЃЌ
AB2=ЃЈOA+OBЃЉ2![]() 75ЃЌ
75ЃЌ
ЁрAB=BCЃЌ
ЁрЁїABCЪЧвдACЮЊЕзЕФЕШбќШ§НЧаЮЃЎ
ЃЈ2ЃЉШчЭМ1жаЃЌЙ§ЕуCЕФжБЯпy![]() НЛxжсгкЕуHЃЌ
НЛxжсгкЕуHЃЌ

Сюy=0ЃЌНтЕУЃКx![]() ЃЌ
ЃЌ
Ёр
ЩшPЃЈmЃЌ![]() 3
3![]() ЃЉЃЌдђQЃЈmЃЌ
ЃЉЃЌдђQЃЈmЃЌ![]() 3
3![]() ЃЉЃЎ
ЃЉЃЎ
Ёпy![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЖдГЦжсЮЊЃКжБЯпx![]() ЃЌ
ЃЌ
ЁрQP=ЃЈ![]() 3
3![]() ЃЉЉЃЈ
ЃЉЉЃЈ![]() 3
3![]() ЃЉ
ЃЉ![]() ЃЌNP=m
ЃЌNP=m![]() ЃЌ
ЃЌ
ЁрОиаЮPQMNЕФжмГЄCОиаЮPQMN=2ЃЈQP+NPЃЉ=2ЃЈ![]() ЃЉ
ЃЉ![]() ЃЛ
ЃЛ
Ёп![]() 0ЃЌПЊПкЯђЯТЃЌ
0ЃЌПЊПкЯђЯТЃЌ
ЁрЕБm=3![]() ЪБЃЌCОиаЮPQMNзюаЁЃЌДЫЪБЃЌPЃЈ3
ЪБЃЌCОиаЮPQMNзюаЁЃЌДЫЪБЃЌPЃЈ3![]() ЃЌЉ3
ЃЌЉ3![]() ЃЉЃЎ
ЃЉЃЎ
ЁпRЮЊЯпЖЮCPЕФжаЕуЃЌ
ЁрRЃЈ![]() ЃЌЉ3
ЃЌЉ3![]() ЃЉЃЌзїЕуRЙигкyжсЖдГЦЕуR'ЃЈ
ЃЉЃЌзїЕуRЙигкyжсЖдГЦЕуR'ЃЈ![]() ЃЌЉ3
ЃЌЉ3![]() ЃЉЃЌДЫЪБRгыNжиКЯЃЌ
ЃЉЃЌДЫЪБRгыNжиКЯЃЌ
гЩЬтвтжЊЃКЖЏЕуGдЫЖЏЕФзюЩйЪБМфt=RK+KT![]() TBЃЌ
TBЃЌ
дкyжсе§АыжсЩЯШЁЕуSЃЈ0ЃЌ4ЃЉЃЌСЌНгжБЯпBSЃЌдђжБЯпBSНтЮіЪНЮЊЃКy![]() x+4ЃЌ
x+4ЃЌ
Й§ЕуR'зїR'JЁЭBSгкJЃЌНЛyжсгкKЃЌНЛxжсгкTЃЌдђR'JМДЮЊЫљЧѓЃЎ
ЁпtanЁЯSBO![]() ЃЌ
ЃЌ
ЁрЁЯSBO=30ЁуЃЌ
ЁрTJ![]() TB
TB
МДt=R'K+KT+TJЃЎ
ЁпRR'=3![]() ЃЌЁЯRR'J=ЁЯBTJ=60ЁуЃЌ
ЃЌЁЯRR'J=ЁЯBTJ=60ЁуЃЌ
ЁрЁїKRR'ЮЊЕШБпШ§НЧаЮЃЌЁЯRKR'=ЁЯKRR'=60ЁуЃЌ
ЁрЁЯKRM=ЁЯKHR=30ЁуЃЌ
ЁрR'J=2RR'=6![]() ЃЛ
ЃЛ
МДЖЏЕуGдЫЖЏЕФзюЩйЪБМфt=6![]() ЃЈУыЃЉЃЛ
ЃЈУыЃЉЃЛ
ЁпЁїJMTЁзЁїJRR'ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЁрTM=3![]() 3ЃЌ
3ЃЌ
ЁрTЃЈ![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
ЃЈ3ЃЉЂйЕБAA'=A'BЪБЃЌШчЭМ2жаЃЌ

ДЫЪБЃЌA'дкЖдГЦжсЩЯ
ЖдГЦадПЩжЊЁЯAC'E=ЁЯA'C'EЃЌ
гжЁЯHEC'=ЁЯA'C'EЃЌ
ЁрЁЯAC'E=ЁЯHEC'ЃЌ
ЁрHE=HC'=5![]() ЃЌ
ЃЌ
ЁрOE=HEЉHO![]() ЃЌ
ЃЌ
Ёр![]()
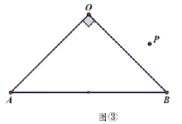
ЂкЕБAA'=ABЪБЃЌШчЭМ3жаЃЌЩшAЁхC'НЛyжсгкJЃЎ

ДЫЪБAA'=AB=BC'=A'C'ЃЌ
ЁрЫФБпаЮA'ABC'ЮЊСтаЮ
гЩЖдГЦадПЩжЊЃКЁЯAC'E=ЁЯA'C'E=30ЁуЃЌ
ЁрJE![]() ЃЌ
ЃЌ
ЁрOE=OJЉJE=6ЃЌ
ЁрEЃЈ0ЃЌ6ЃЉЃЛ
ЂлЕБAA'=A'BЪБЃЌШчЭМ4жаЃЌЩшAC'НЛyжсгкMЃЎ

ДЫЪБЃЌA'дкЖдГЦжсЩЯЁЯMC'E=75Ёу
гжЁЯAMO=ЁЯEMC'=30ЁуЃЌ
ЁрЁЯMEC'=75ЁуЃЌ
ЁрME=MC'ЃЌ
ЁрMC'![]() ЃЌ
ЃЌ
ЁрOE![]() ЃЌ
ЃЌ
ЁрEЃЈ![]() ЃЉЃЛ
ЃЉЃЛ
ЂмЕБA'B=ABЪБЃЌШчЭМ5жаЃЌ

ДЫЪБAC'=A'C'=A'B=ABЃЌ
ЁрЫФБпаЮAC'A'BЮЊСтаЮ
гЩЖдГЦадПЩжЊЃЌC'ЃЌEЃЌBЙВЯпЃЌ
ЁрOE![]() ЃЌ
ЃЌ
ЁрEЃЈ0ЃЌ12ЃЉЃЎ
злЩЯЫљЪіПЩЕУЃКЕуEзјБъЮЊЃЈ0ЃЌ3![]() ЃЉЛђЃЈ0ЃЌ6ЃЉЛђЃЈ0ЃЌ3
ЃЉЛђЃЈ0ЃЌ6ЃЉЛђЃЈ0ЃЌ3![]() ЃЉЛђЃЈ0ЃЌ12ЃЉЃЎ
ЃЉЛђЃЈ0ЃЌ12ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌвдЕу
ЕФжаЕуЃЌвдЕу![]() ЮЊдВаФзїдВаФНЧЮЊ
ЮЊдВаФзїдВаФНЧЮЊ![]() ЕФЩШаЮ
ЕФЩШаЮ![]() ЃЌЕу
ЃЌЕу![]() ЧЁдкЛЁ
ЧЁдкЛЁ![]() ЩЯЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЃЈ ЃЉ
ЩЯЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
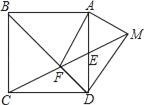
ЁОЬтФПЁПШчЭМЃЌБпГЄЮЊ4е§ЗНаЮABCDжаЃЌEЮЊБпADЕФжаЕуЃЌСЌНгЯпЖЮECНЛBDгкЕуFЃЌЕуMЪЧЯпЖЮCEбгГЄЯпЩЯЕФвЛЕуЃЌЧвЁЯMAFЮЊжБНЧЃЌдђDMЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊТњзуЪаГЁашЧѓЃЌФГГЌЪадкЮхдТГѕЮхЁАЖЫЮчНкЁБРДСйЧАЯІЃЌЙКНјвЛжжЦЗХЦєезгЃЌУПКаНјМлЪЧ40дЊЃЎГЌЪаЙцЖЈУПКаЪлМлВЛЕУЩйгк45дЊЃЎИљОнвдЭљЯњЪлОбщЗЂЯжЃЛЕБЪлМлЖЈЮЊУПКа45дЊЪБЃЌУПЬьПЩвдТєГі700КаЃЌУПКаЪлМлУПЬсИп1дЊЃЌУПЬьвЊЩйТєГі20КаЃЎ
ЃЈ1ЃЉЪдЧѓГіУПЬьЕФЯњЪлСПyЃЈКаЃЉгыУПКаЪлМлxЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕБУПКаЪлМлЖЈЮЊЖрЩйдЊЪБЃЌУПЬьЯњЪлЕФРћШѓPЃЈдЊЃЉзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉЮЊЮШЖЈЮяМлЃЌгаЙиЙмРэВПУХЯоЖЈЃКетжжєезгЕФУПКаЪлМлВЛЕУИпгк58дЊЃЎШчЙћГЌЪаЯывЊУПЬьЛёЕУВЛЕЭгк6000дЊЕФРћШѓЃЌФЧУДГЌЪаУПЬьжСЩйЯњЪлєезгЖрЩйКаЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
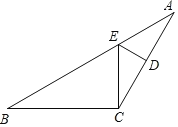
ЁОЬтФПЁПШчЭМЃЌдкЕШбќЁїABCжаЃЌAC=BCЃЌЁЯACB=4ЁЯBЃЌЕуDЪЧACБпЕФжаЕуЃЌDEЁЭACЃЌНЛABгкЕуEЃЌСЌНгCEЃЎ
ЃЈ1ЃЉЧѓЁЯBCEЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЧѓжЄЃКAB=3CEЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГѕжабЇаЃОйаааЃдАИшГЊДѓШќЃЌЖдИїФъМЖЭЌбЇЕФЛёНБЧщПіНјааСЫЭГМЦЃЌВЂЛцжЦСЫШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыНсКЯЭМжаЯрЙиЪ§ОнНтД№ЯТСаЬтЃК
ЃЈ1ЃЉЧыНЋЬѕаЮЭГМЦЭМВЙШЋЃЛ
ЃЈ2ЃЉЛёЕУвЛЕШНБЕФЭЌбЇжага![]() РДздЦпФъМЖЃЌга
РДздЦпФъМЖЃЌга![]() РДздАЫФъМЖЃЌЦфЫћЭЌбЇОљРДздОХФъМЖЃЌЯжзМБИДгЛёЕУвЛЕШНБЕФЭЌбЇжаШЮбЁСНШЫВЮМгШЋЪааЃдАИшГЊДѓШќЃЌЧыЭЈЙ§СаБэЛђЛЪїзДЭМЧѓЫљбЁГіЕФСНШЫжагаЦпФъМЖЛђАЫФъМЖЭЌбЇЕФИХТЪЃЎ
РДздАЫФъМЖЃЌЦфЫћЭЌбЇОљРДздОХФъМЖЃЌЯжзМБИДгЛёЕУвЛЕШНБЕФЭЌбЇжаШЮбЁСНШЫВЮМгШЋЪааЃдАИшГЊДѓШќЃЌЧыЭЈЙ§СаБэЛђЛЪїзДЭМЧѓЫљбЁГіЕФСНШЫжагаЦпФъМЖЛђАЫФъМЖЭЌбЇЕФИХТЪЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
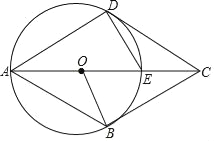
ЁОЬтФПЁПвбжЊЃЌЫФБпаЮABCDжаЃЌEЪЧЖдНЧЯпACЩЯвЛЕуЃЌDEЃНECЃЌвдAEЮЊжБОЖЕФЁбOгыБпCDЯрЧагкЕуDЃЌЕуBдкЁбOЩЯЃЌСЌНгOBЃЎ
ЃЈ1ЃЉЧѓжЄЃКDEЃНOEЃЛ
ЃЈ2ЃЉШєCDЁЮABЃЌЧѓжЄЃКBCЪЧЁбOЕФЧаЯпЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЧѓжЄЃКЫФБпаЮABCDЪЧСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЌЖЏЕу
ЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂби
ГіЗЂби![]() ЯђжеЕу
ЯђжеЕу![]() дЫЖЏЃЌЖЏЕу
дЫЖЏЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂбиелЯп
ГіЗЂбиелЯп![]() ЯђжеЕу
ЯђжеЕу![]() дЫЖЏЃЌСНЕуЫйЖШОљЮЊУПУы1ИіЕЅЮЛЃЌСНЕуЭЌЪБГіЗЂЃЌЕБЦфжавЛЕуЕНДяжеЕуКѓЃЌдЫЖЏЭЃжЙЃЌЩшдЫЖЏЪБМфЮЊ
дЫЖЏЃЌСНЕуЫйЖШОљЮЊУПУы1ИіЕЅЮЛЃЌСНЕуЭЌЪБГіЗЂЃЌЕБЦфжавЛЕуЕНДяжеЕуКѓЃЌдЫЖЏЭЃжЙЃЌЩшдЫЖЏЪБМфЮЊ![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЈЦНЗНЕЅЮЛЃЉЃЌдђ
ЃЈЦНЗНЕЅЮЛЃЉЃЌдђ![]() гы
гы![]() жЎМфЕФЭМЯѓДѓжТЮЊЃЈ ЃЉ
жЎМфЕФЭМЯѓДѓжТЮЊЃЈ ЃЉ
A. B.
B. C.
C. D.
D.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЭтвЛЕуЃЌНЋ
ЭтвЛЕуЃЌНЋ![]() ШЦЕу
ШЦЕу![]() АДЫГЪБеыЗНЯђа§зЊ
АДЫГЪБеыЗНЯђа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЌЧвЕу
ЃЌЧвЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕудкЭЌвЛжБЯпЩЯ.
Ш§ЕудкЭЌвЛжБЯпЩЯ.
ЃЈ1ЃЉЃЈЙлВьВТЯыЃЉ
дкЭМЂйжаЃЌ![]() ЃЛдкЭМЂкжаЃЌ
ЃЛдкЭМЂкжаЃЌ![]() ЃЈгУКЌ
ЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉ
ЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉЃЈРрБШЬНОПЃЉ
ШчЭМЂлЃЌШє![]() ЃЌЧыВЙШЋЭМаЮЃЌдйЙ§Еу
ЃЌЧыВЙШЋЭМаЮЃЌдйЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЬНОПЯпЖЮ
ЃЌЬНОПЯпЖЮ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ3ЃЉЃЈЮЪЬтНтОіЃЉ
Шє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕН
ЕН![]() ЕФОрРы.
ЕФОрРы.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com