
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
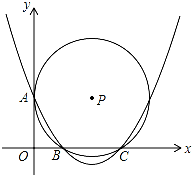 已知:如图,在平面直角坐标系xOy中,点A(0,$\sqrt{3}$),点B(1,0),点C(3,0),以点P为圆心的圆与y轴相切于点A,与x轴相交于B、C两点(点B在点C的左边).
已知:如图,在平面直角坐标系xOy中,点A(0,$\sqrt{3}$),点B(1,0),点C(3,0),以点P为圆心的圆与y轴相切于点A,与x轴相交于B、C两点(点B在点C的左边).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
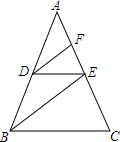 请把下列解题过程补充完整,并在括号内注明理由.
请把下列解题过程补充完整,并在括号内注明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
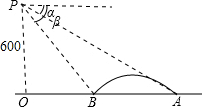 如图,直升飞机在大桥AB的上方P点处,此时飞机离地面高度PO=600米,且A、B、O三点在一条直线上,测得大桥两端A、B的俯角分别为α=30°,β=45°,求大桥的长AB.
如图,直升飞机在大桥AB的上方P点处,此时飞机离地面高度PO=600米,且A、B、O三点在一条直线上,测得大桥两端A、B的俯角分别为α=30°,β=45°,求大桥的长AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
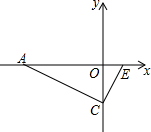 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C(0,-2).如果BC=$\sqrt{5}$,∠ACB=90°.求这个二次函数解析式.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C(0,-2).如果BC=$\sqrt{5}$,∠ACB=90°.求这个二次函数解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com