
【题目】若凸四边形的两条对角线所夹锐角为60°,我们称这样的凸四边形为“完美四边形”.
(1)①在“平行四边形、梯形、菱形、正方形”中,一定不是“完美四边形”的有 ;
②若矩形ABCD是“完美四边形”,且AB=4,则BC= ;
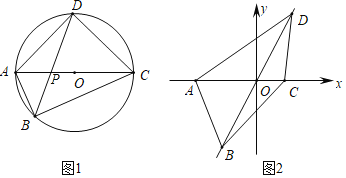
(2)如图1,“完美四边形”ABCD内接于⊙O,AC与BD相交于点P,且对角线AC为直径,AP=1,PC=5,求另一条对角线BD的长;
(3)如图2,平面直角坐标系中,已知“完美四边形”ABCD的四个顶点A(﹣3,0)、C (2,0),B在第三象限,D在第一象限,AC与BD交于点O,直线BD的斜率为![]() ,且四边形ABCD的面积为15
,且四边形ABCD的面积为15![]() ,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.
,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.
【答案】(1)①菱形、正方形;②4![]() 或
或![]() ;(2)BD=2
;(2)BD=2![]() ;(3)a的值为
;(3)a的值为![]() 或
或![]() .
.
【解析】
(1)①由菱形、正方形的对角线互相垂直即可判断.
②矩形ABCD对角线相等且互相平分,再加上对角线夹角为60°,即出现等边三角形,所以得到矩形相邻两边的比等于tan60°.由于AB边不确定是较长还是较短的边,故需要分类讨论计算.
(2)过O点作OH垂直BD,连接OD,由∠DPC=60°可求得OH,在Rt△ODH中勾股定理可求DH,再由垂径定理可得BD=2DH.
(3)由BD与x轴成60°角可知直线BD解析为y=![]() x,由二次函数图象与x轴交点为A、C可设解析式为y=a(x+3)(x-2),把两解析式联立方程组,消去y后得到关于x的一元二次方程,解即为点B、D横坐标,所以用韦达定理得到xB+xD和xBxD进而得到用a表示的(xB-xD)2.又由四边形面积可求得xB-xD=6,即得到关于a的方程并解方程求得a.
x,由二次函数图象与x轴交点为A、C可设解析式为y=a(x+3)(x-2),把两解析式联立方程组,消去y后得到关于x的一元二次方程,解即为点B、D横坐标,所以用韦达定理得到xB+xD和xBxD进而得到用a表示的(xB-xD)2.又由四边形面积可求得xB-xD=6,即得到关于a的方程并解方程求得a.
(1)①∵菱形、正方形的对角线互相垂直,
∴菱形、正方形不是“美丽四边形”.
故答案为:菱形、正方形.
②设矩形ABCD对角线相交于点O
∴AC=BD,AO=CO,BO=DO,∠ABC=90°,
∴AO=BO=CO=DO,
∵矩形ABCD是“美丽四边形”,
∴AC、BD夹角为60°,
i)如图1,若AB=4为较短的边,则∠AOB=60°,

∴△OAB是等边三角形
∴∠OAB=60°
∴Rt△ABC中,tan∠OAB=![]() ,
,
∴BC=![]() AB=4
AB=4![]() ,
,
ii)如图2,若AB=4为较长的边,则∠BOC=60°,

∴△OBC是等边三角形,
∴OCB=60°,
∴Rt△ABC中,tan∠OCB=![]() =
=![]() ,
,
∴BC=![]() =
=![]() .
.
(2)过点O作OH⊥BD于点H,连接OD

∴∠OHP=∠OHD=90°,BH=DH=![]() BD,
BD,
∵AP=1,PC=5
∴⊙O直径AC=AP+PC=6
∴OA=OC=OD=3
∴OP=OA﹣AP=3﹣1=2
∵四边形ABCD是“美丽四边形”
∴∠OPH=60°,
∴Rt△OPH中,sin∠OPH=![]() ,
,
∴OH=![]() =
=![]() ,
,
∴Rt△ODH中,DH=![]() =
=![]() =
=![]() ,
,
∴BD=2DH=2![]() .
.
(3)过点B作BM⊥x轴于点M,过点D作DN⊥x轴于点N

∴∠BMO=∠DNO=90°
∵直线BD的斜率为![]() ,
,
∴直线BD解析式为y=![]() x,
x,
∵二次函数的图象过点A(﹣3,0)、C(2,0),即与x轴交点为A、C
∴用交点式设二次函数解析式为y=a(x+3)(x﹣2)
∵ ,
,
整理得:ax2+(a﹣![]() )x﹣6a=0,
)x﹣6a=0,
∴xB+xD=﹣![]() ,xBxD=﹣6
,xBxD=﹣6
∴(xB﹣xD)2=(xB+xD)2﹣4xBxD=(﹣![]() )2+24
)2+24
∵S四边形ABCD=S△AB+S△ACD=![]() ACBM+
ACBM+![]() ACDN=
ACDN=![]() AC(BM+DN)=
AC(BM+DN)=![]() AC(yD﹣yB)=
AC(yD﹣yB)=![]() AC(
AC(![]() xD﹣
xD﹣![]() xB)=
xB)=![]() (xB﹣xD).
(xB﹣xD).
∴![]() (xB﹣xD)=15
(xB﹣xD)=15![]() ,
,
∴xB﹣xD=6,
∴(﹣![]() )2+24=36,
)2+24=36,
解得:a1=![]() ,a2=
,a2=![]() .
.
∴a的值为![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】万州区中小学社会活动实践基地开展了人与社会、人与自然、人与自我的综合实践活动,其中高空项目能培养学生不怕困难,不畏艰险的精神.在高空项目中有以下四个特色实践活动:“A.合力制胜,B.空中断桥,C.绝壁飞胎,D.天罗地网”.为了解学生最喜爱哪项综合实践活动,随机抽取部分学生进行问卷调查(每位学生只能选择一项),将调查结果绘制成下面两幅不完整的统计图,请结合图中提供的信息回答下列问题:
(1)本次一共调查了 名学生,并补全条形统计图;
(2)现有最喜爱A,B,C,D活动项目的学生各一人,学校要从这四人中随机选取两人交流活动体会,请用列表或画树状图的方法求出恰好选取最喜爱C和D项目的两位学生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到正方形
后得到正方形![]() ,依此方式,绕点
,依此方式,绕点![]() 连续旋转2019次得到正方形
连续旋转2019次得到正方形![]() ,如果点
,如果点![]() 的坐标为(1,0),那么点
的坐标为(1,0),那么点![]() 的坐标为________.
的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+bx+c=0.
(1)若b=2m﹣1,m+c=﹣6,判断方程根的情况;
(2)若方程有两个相等的非零实数根,且b2﹣c2﹣4=0,求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1,以下结论:①abc>0;②3a+c>0;③m为任意实数,则有a(m2+1)+bm≥0;④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2,正确的有( )个.
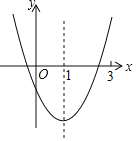
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
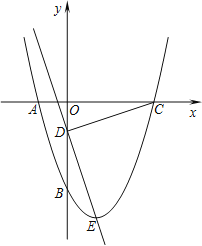
【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.
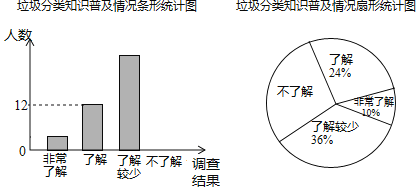
(1)求:本次被调查的学生有多少名?补全条形统计图.
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是多少.
(3)被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
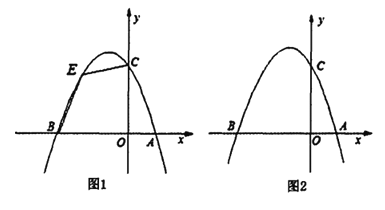
【题目】如图1,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(l)求抛物线的表达式;
(2)如图l,若点![]() 为第二象限抛物线上一动点,连接
为第二象限抛物线上一动点,连接![]() ,求四边形
,求四边形![]() 面积的最大值,并求此时
面积的最大值,并求此时![]() 点的坐标;
点的坐标;
(3)如图2,在![]() 轴上是否存在一点
轴上是否存在一点![]() 使得
使得![]() 为等腰三角形?若存在,请求出所有符合条件的点
为等腰三角形?若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
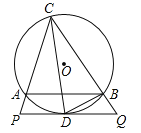
【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程![]() 的两实根,且tan∠PCD=
的两实根,且tan∠PCD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com