
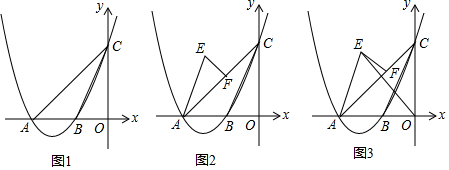
���� ��1�������OB������ʾ��OA��OC�����á�ABC����������������OA��OB��OC�����ɵó���A��B��C�����꣬����ô���ϵ������������ߵĽ���ʽ��
��2�������õ���ֱ�������ε����ʵó�EP=-$\sqrt{2}$t���������Ǻ�����ʾ��AF��������ʾ��PF������d��ʾ��EP���������̼��ɵó����ۣ�
��3�������tan��AEG=$\frac{1}{3}$�����жϳ���AEM�ա�HQI�������ó�AM=HI=$\frac{1}{3}$EM����$\frac{OI}{IM}=\frac{1}{2}$��OI=m����IM=2m��AM=5-3m�ó�H��-m��5-3m�����������߽���ʽ���m���������EM=6���ɣ�
��� �⣺��1����OB=x����OA=OC=$\frac{5}{2}$x��
�ߡ�ABC�����Ϊ$\frac{15}{2}$��
��$\frac{1}{2}$��$\frac{5}{2}$x-x��•$\frac{5}{2}$x=$\frac{15}{2}$
��x=2��-2���ᣩ��
��OA=OC=5��OB=2��
��A��-5��0����B��-2��0����C��0��5����
�������߽���ʽΪy=a��x+5����x+2��=ax2+7ax+10a��
��10a=5��
��a=$\frac{1}{2}$
�����߽���ʽy=$\frac{1}{2}$x2+$\frac{7}{2}$x+5��
��2����ͼ2��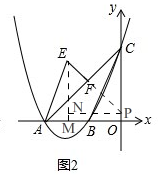 ��EM��OA��M���ӳ�EF��y����P����P��PN��EM��N��
��EM��OA��M���ӳ�EF��y����P����P��PN��EM��N��
��E�ĺ�����Ϊt��
��PN=-t��
���EPN=90��-��CPF=45�㣬
��EP=-$\sqrt{2}$t��
��Rt��AEF��EF=d��tan��CAE=$\frac{1}{2}$��
��AF=2d��
��OA=OC=5��
��AC=5$\sqrt{2}$����ACO=45�㣬
��CF=AC-AF=5$\sqrt{2}$-2d��
��EF��AC����ACO=45�㣬
��PF=CF=5$\sqrt{2}$-2d��
��EP=EF+PF=5$\sqrt{2}$-2d=-$\sqrt{2}$t��
��d=5$\sqrt{2}$+2t
��3����ͼ3�� ����E��EM��AB��M��AC��G��
����E��EM��AB��M��AC��G��
�ߡ�HQA+��CAE=45�㣬
�֡ߡ�AEM+��CAE=45�㣬��HQA+��CAE=45�㣬
���AEM=��HQA
�ڡ�AFG�У�FG=EF=d��
��AG=AF-FG=2d-d=d��EG=$\sqrt{2}$EF=$\sqrt{2}$d��
�ڵ���ֱ��������AMG�У�AM=GM=$\frac{\sqrt{2}}{2}$AG=$\frac{\sqrt{2}}{2}$d��
��EM=EG+GM=$\frac{3\sqrt{2}}{2}$d��
��Rt��AEM��tan��AEG=$\frac{AM}{EM}$=$\frac{1}{3}$��
��H��HI��x����I��
�ڡ�AEM�͡�HQI�У�$\left\{\begin{array}{l}{��AME=��HIQ=90��}\\{��AEM=��HQI}\\{AE=HQ}\end{array}\right.$��
��AEM�ա�HQI��
��EM=QI��AM=HI=$\frac{1}{3}$EM��
��$\frac{OI}{IM}=\frac{1}{2}$
��OI=m����IM=2m��AM=5-3m��
��H��-m��5-3m��
���������߽���ʽy=$\frac{1}{2}$x2+$\frac{7}{2}$x+5�У���m1=1��m2=0����ȥ����
��I��-1��0����AM=2��
��EM=$\frac{3\sqrt{2}}{2}$d=3AM=6��
��Q��n��0����
��QI=|-1-n|=|n+1|��
��QI=EM=6��
��n+1=��6��
��n=-7��5��
��Q1��5��0����Q2��-7��0����
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ����������ֱ�������ε��ж������ʣ�ȫ�������ε��ж������ʣ�������Ǻ����Ķ��壬�⣨1���Ĺؼ��������A��B��C�����꣬�⣨2���Ĺؼ����������������PF=CF=5$\sqrt{2}$-2d���⣨3���Ĺؼ���tan��AEG=$\frac{AM}{EM}$=$\frac{1}{3}$����һ���ۺ��ԱȽ�ǿ���п������⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
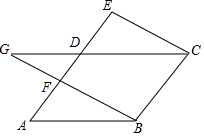 ��ͼ����?ABCD�У�AD=4��AB=5���ӳ�AD����E������EC����B��BF��CE��AD�ڵ�F����CD���ӳ����ڵ�G��
��ͼ����?ABCD�У�AD=4��AB=5���ӳ�AD����E������EC����B��BF��CE��AD�ڵ�F����CD���ӳ����ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
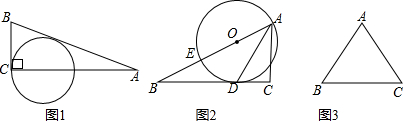
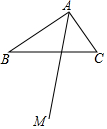 ��ͼ����Rt��ABC�У���BAC=90�㣬AB��AC������AMƽ�֡�BAC��
��ͼ����Rt��ABC�У���BAC=90�㣬AB��AC������AMƽ�֡�BAC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
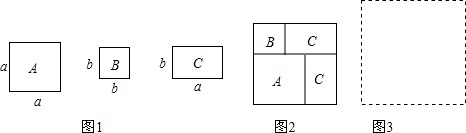
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
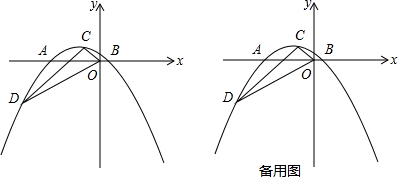
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com