
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表所示.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
下列说法:①抛物线与y轴的交点为(0,6); ②抛物线的对称轴在y轴的右侧;③抛物线一定经过点(3,0);④在对称轴左侧,y随x增大而减小.⑤不等式ax2+(b﹣3)x+c﹣6>0解集为﹣2<x<0.其中说法正确的有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
【答案】D
【解析】
由表格可知(0,6),(1,6)两点纵坐标相等,抛物线对称轴为x=![]() =
=![]() ,且抛物线开口向下,根据抛物线的开口方向,对称轴解题.
,且抛物线开口向下,根据抛物线的开口方向,对称轴解题.
解:观察表格可知,抛物线与y轴的交点为(0,6),故①正确;
观察表格可知,抛物线对称轴为x=![]() =
=![]() >0,对称轴在y轴的右侧,故②正确;
>0,对称轴在y轴的右侧,故②正确;
抛物线的对称轴为x=![]() ,点(﹣2,0)的对称点是(3,0),所以抛物线一定经过点(3,0),故③正确;
,点(﹣2,0)的对称点是(3,0),所以抛物线一定经过点(3,0),故③正确;
观察表格可知,对称轴左侧,y随x增大而增大,故④错误;
整理得ax2+bx+c>3x+6,
∵直线y=3x+6与x轴的交点为(﹣2,0),与y轴的交点为(0,6),
∴直线y=3x+6与抛物线y=ax2+bx+c的交点为(2,0),(0,6),
由表格可知抛物线开口向下,
∴不等式ax2+(b﹣3)x+c﹣6>0解集为﹣2<x<0,故⑤正确;
故选:D.


科目:初中数学 来源: 题型:
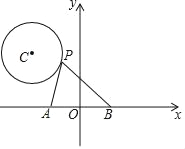
【题目】如图,在平面直角坐标系中,点P是以C(﹣![]() ,
,![]() )为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是_____.
)为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
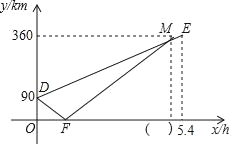
【题目】A,B,C三地在同一条公路上,A地在B,C两地之间,甲、乙两车同时从A地出发匀速行驶,甲车驶向C地,乙车先驶向B地,到达B地后,调头按原速经过A地驶向C地(调头时间忽略不计),到达C地停止行驶,甲车比乙车晚0.4小时到达C地,两车距B地的路程y(km)与行驶时间x(h)之间的函数关系如图所示,请结合图象信息,解答下列问题:
(1)甲车行驶的速度是 km/h,并在图中括号内填入正确的数值;
(2)求图象中线段FM所表示的y与x的函数解析式(不需要写出自变量x的取值范围);
(3)在乙车到达C地之前,甲、乙两车出发后几小时与A地路程相等?直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料,每瓶进价为10元.经市场调查表明,当售价在12元到14元之间(含12元,14元)浮动时,日均销售y(瓶)与售价x(元)之间的关系可近似的看作一次函数,且当x=10时,y=500;x=12,y=400.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)应将售价定为每瓶多少元时,所得日均毛利润最大?最大日均毛利润为多少元?(每瓶毛利润=每瓶售价﹣每瓶进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
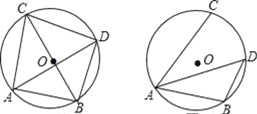
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+(2﹣a)x﹣2(a>0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.给出下列结论:
①在a>0的条件下,无论a取何值,点A是一个定点;
②在a>0的条件下,无论a取何值,抛物线的对称轴一定位于y轴的左侧;
③y的最小值不大于﹣2;
④若AB=AC,则a=![]() .
.
其中正确的结论有( )个.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“植树节”期间,小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动,规则如下:在两个盒子内分别装入标有数字1,2,3,4的四个和标有数字1,2,3的三个完全相同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于5,那么小王去,否则就是小李去.
(1)用树状图或列表法求出小王去的概率;
(2)小李说:“这种规则不公平”,你认同他的说法吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com