
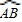 上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH=
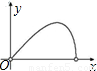
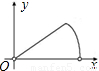
上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH= DE.设EC的长为x,△CEH的面积为y,选项中表示y与x的函数关系式的图象可能是( )
DE.设EC的长为x,△CEH的面积为y,选项中表示y与x的函数关系式的图象可能是( )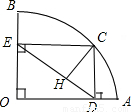

 x,表示出FH的长,进而得出△CEH的面积,根据图象得出符合要求的图象.
x,表示出FH的长,进而得出△CEH的面积,根据图象得出符合要求的图象.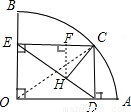 解:连接OC,作HF⊥EC于一点F,
解:连接OC,作HF⊥EC于一点F, DE,
DE, x,
x,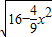 =
=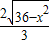 ,
, ×
×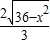 x,
x,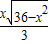 ,
,

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
 是
是 | AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
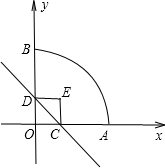
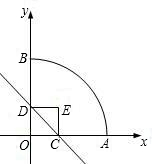 标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则:
标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 是______;
是______; 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.查看答案和解析>>
科目:初中数学 来源:第3章《圆》中考题集(81):3.4 弧长和扇形的面积,圆锥的侧面展开图(解析版) 题型:解答题
 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.
查看答案和解析>>
科目:初中数学 来源:2006年福建省福州市中考数学试卷(大纲卷)(解析版) 题型:解答题
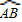 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com