
【题目】在△ABC中,AB=17,BC=21,AC=10,动点P从点C出发,沿着CB运动,速度为每秒3个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:
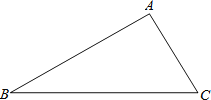
(1)求BC上的高;
(2)当t为何值时,△ACP为等腰三角形?
【答案】(1)8;(2)![]() ;4;
;4;![]() .
.
【解析】
(1)过点A作AD⊥BC于点D,设CD=x,则BD=21﹣x,再根据勾股定理求出x的值,进而可得出AD的长;
(2)分AC=PC,AP=AC及AP=PC三种情况进行讨论.
(1)过点A作AD⊥BC于点D,设CD=x,则BD=21-x,
∵△ABD与△ACD均为直角三角形,
∴AB2-BD2=AC2-CD2,即172-(21-x)2=102-x2,解得x=6,
∴AD=![]() =
=![]() =8,
=8,
故答案为:8;
(2)当AC=PC时,
∵AC=10,
∴AC=PC=10,
∴t=![]() 秒;
秒;
当AP=AC时,过点A作AD⊥BC于点D,由(1)知,CD=6,
∴PC=12,
∴t=![]() =4秒;
=4秒;
当AP=PC时,过点P作PE⊥AC于点E,
∵AC=10,
∴CE=5,
∴![]() ,即
,即![]() =
=![]() ,解得PC=
,解得PC=![]() ,
,
 (秒)
(秒)
综上所述,t=![]() 秒或4秒或
秒或4秒或![]() 秒,
秒,
故答案为:![]() ;4;
;4;![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】小明和小丽在做游戏:有A、B两个不透明的布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字0,1,2,3,B布袋中有四个除标号外完全相同的小球,小球上分别标有数字1,2,3.先从A布袋中随机取出一个小球,用m表示取出的球上的标号,再从B布袋中随机取出一个小球,用n表示取出的球上的标号.规定当m+n为偶数时小明获胜,否则小丽获胜,请用树状图或列表法,求出小明获胜的概率,并说明这个游戏是否公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生的校园文化生活,珠海第十中学举办了“十中好声音”才艺比赛,三个年级都有男、女各一名选手进入决赛.初一年级选手编号为男1号、女1号,初二年级选手编号为男2号、女2号,初三年级选手编号为男3号、女3号.比赛规则是男、女各一名选手组成搭档展示才艺.
(1)用列举法说明所有可能出现搭挡的结果;
(2)求同一年级男、女选手组成搭档的概率;
(3)求高年级男选手与低年级女选手组成搭档的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=11,AC=5,则BE的长( )
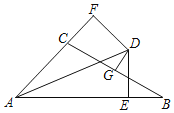
A.3B.2C.5D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生课外活动,某校积极开展社团活动,开设的体育社团有:A:篮球,B:排球,C:足球,D:羽毛球,E:乒乓球.学生可根据自己的爱好选择一项,李老师对八年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )
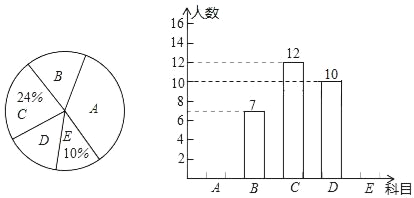
A. 选科目E的有5人
B. 选科目A的扇形圆心角是120°
C. 选科目D的人数占体育社团人数的![]()
D. 据此估计全校1000名八年级同学,选择科目B的有140人
查看答案和解析>>
科目:初中数学 来源: 题型:
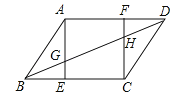
【题目】如图,在平行四边形ABCD中,AE⊥BC,CF⊥AD,垂足分别为E,F,AE,CF分别与BD交于点G和H,且AB=![]() .
.
(1)若tan∠ABE =2,求CF的长;
(2)求证:BG=DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块含30°角的直角三角板OAB和一块等腰直角三角板ODC按如图的方式放置在平面直角坐标系中.已知C、B两点分别在x轴和y轴上,∠ABO=∠D=90°,OB=OC,AB=3.
(1)求边OC的长.
(2)将直角三角板OAB绕点顺时针方向旋转,使OA落在x轴上的OA′位置,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人的某一人.
(1)求第二次传球后球回到甲手里的概率.
(2)如果甲跟另外n(n≥2)个人做(1)同样的游戏,那么,第三次传球后球回到甲手里的概率是 .(请用含n的式子直接写结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com