
����Ŀ������С������12�֣�
��֪����Rt��ABC��Rt��DEF����ͼ��1���ڷţ���C���E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���ACB = ��EDF = 90�㣬��DEF = 45����AC = 8 cm��BC = 6 cm��EF = 9 cm��
��ͼ��2������DEF��ͼ��1����λ�ó�������1 cm/s���ٶ���CB����ABC��������������DEF������ͬʱ����P����ABC�Ķ���B��������2 cm/s���ٶ���BA���A��������.����DEF�Ķ���D�ƶ���AC����ʱ����DEFֹͣ��������PҲ��ֹ֮ͣ�ƶ���DE��AC�ཻ�ڵ�Q������PQ��������ʱ��Ϊt��s����0��t��4.5����
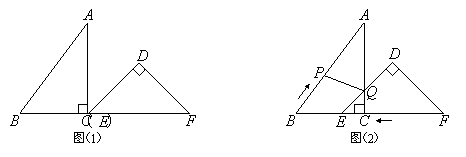
����������⣺
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2������PE�����ı���APEC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ���Ƿ����ijһʱ��t��ʹ���y��С�������ڣ����y����Сֵ���������ڣ�˵�����ɣ�
��3���Ƿ����ijһʱ��t��ʹP��Q��F������ͬһ��ֱ���ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
���𰸡�
��1��t=2
��2����t = 3ʱ��y��С=![]()
��3����t = 1s����P��Q��F������ͬһ��ֱ����
��������
�⣺��1������A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��AP = AQ.
�ߡ�DEF = 45������ACB = 90�㣬��DEF����ACB����EQC = 180����
���EQC = 45��.
���DEF =��EQC.
��CE = CQ.
������֪��CE = t��BP =2 t��
��CQ = t.
��AQ = 8��t.
��Rt��ABC�У��ɹ��ɶ����ã�AB = 10 cm .
��AP = 10��2 t.
��10��2 t = 8��t.
��ã�t = 2.
�𣺵�t = 2 sʱ����A���߶�PQ�Ĵ�ֱƽ������. 4��
��2����P��![]() ����BE��M����
����BE��M����![]() .
.
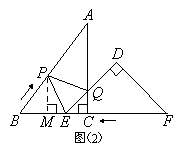
��Rt��ABC��Rt��BPM��![]() ��
��
��![]() . ��PM =
. ��PM = ![]() .
.
��BC = 6 cm��CE = t�� �� BE = 6��t.
��y = S��ABC��S��BPE =![]() ��
��![]() =
= ![]() ��
��![]()
=![]() =
= ![]() .
.
��![]() ���������߿�������.
���������߿�������.
����t = 3ʱ��y��С=![]() .
.
�𣺵�t = 3sʱ���ı���APEC�������С����С���Ϊ![]() cm2.8��
cm2.8��
��3����������ijһʱ��t��ʹ��P��Q��F������ͬһ��ֱ����.

��P��![]() ����AC��N��
����AC��N��
��![]() .
.
��![]() �����PAN ����BAC.
�����PAN ����BAC.
��![]() .
.
��![]() .
.
��![]() ��
��![]() .
.
��NQ = AQ��AN��
��NQ = 8��t��(![]() ) =
) = ![]() ��
��
�ߡ�ACB = 90�㣬B��C��E����F��ͬһ��ֱ���ϣ�
���QCF = 90������QCF = ��PNQ.
�ߡ�FQC = ��PQN��
���QCF����QNP .
��![]() . ��
. ��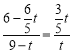 .
.
��![]() ��
��
��ã�t = 1.
�𣺵�t = 1s����P��Q��F������ͬһ��ֱ����. 12��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���Ϊ�������˿ͣ�������ɫ���˽�������ٰ�����Ʒ�н���������������200Ԫ�ߣ������ֽ���������ѡ��һ��ֱ�ӻ��20Ԫ�����ȯ�����ǵõ�һ��ҡ���Ļ��ᣮ��֪��ҡ������װ��2�������2��������ɫ����������ͬ��ҡ���߱����ҡ������һ������ҡ���������������ɫ����������������ȯ�Ķ��٣�
�� | ���� | һ��һ�� | ���� |
���ȯ��Ԫ�� | 18 | 24 | 18 |
��1���������б���������״ͼ������һ������ҡ��һ��һ������ĸ��ʣ�
��2�����һ���˿͵����ڱ��깺����200Ԫ����ֻ���ǻ��������Ʒȯ�������������ѡ�����ַ�����Ϊʵ�ݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ķ���
�ķ���![]()
(1)����������������������������![]() ��ֵ
��ֵ
(2)��![]() ���㲻��ʽ
���㲻��ʽ![]() �������۷��̸��������
�������۷��̸��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB��90������E��F�ڱ�AB�ϣ�����AC��CE���ۣ�ʹ��A����AB�ϵĵ�D�����ٽ���BC��CF���ۣ�ʹ��B����CD���ӳ����ϵĵ�B'����
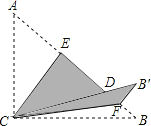
��1�����ECF�Ķ�����
��2����CE��4��B'F��1�����߶�BC�ij�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��a��0��ͼ���һ���֣�x=��1�ǶԳ��ᣬ�������жϣ���b��2a=0����4a��2b+c��0����a��b+c=��9a����������3��y1������![]() ��y2���������������㣬��y1��y2��������ȷ���ǣ� ��
��y2���������������㣬��y1��y2��������ȷ���ǣ� ��
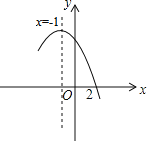
A. �٢ڢ� B. �٢ۢ� C. �٢ڢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
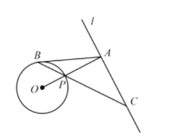
����Ŀ����ͼ����ֱ֪��l���O ���룬OA��l�ڵ�A������O �ڵ�P����B�ǡ�O��һ�㣬����BP���ӳ�����ֱ��l�ڵ�C��ʹ��AB=AC.
��1����֤��AB�ǡ�O�����ߣ�
��2����PC=2![]() ��OA=3�����߶�PB�ij�.
��OA=3�����߶�PB�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() �ᣬ˫����
�ᣬ˫����![]() ��
��![]() ��
��![]() ���㣨
���㣨![]() ������ֱ֪���ϣ�����
������ֱ֪���ϣ�����![]() ����
����![]() ________��
________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���� y=x+1 ��ͼ���� y �ύ�ڵ� A��һ�κ��� y=kx+b ��ͼ���� B��0����1������x �� �Լ� y=x+1 ��ͼ��ֱ��ڵ� C��D���ҵ� D ������Ϊ��1��n����

��1����n= ��k= ��b= ��
��2������ y=kx+b �ĺ���ֵ���ں��� y=x+1 �ĺ���ֵ����X��ȡֵ��Χ�� ��
��3�����ı��� AOCD �������
��4���� x�����Ƿ������ P��ʹ���Ե� P��C��D Ϊ�������������ֱ�������Σ������������ P �����ꣻ ������������˵��������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com