
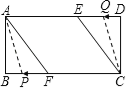
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC与点E、F,垂足为O.

(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
【答案】(1)证明见解析,AF=5cm;(2)t=![]() 秒.
秒.
【解析】试题分析:(1)根据全等推出OE=OF,得出平行四边形AFCE,根据菱形判定推出即可,根据菱形性质得出AF=CF,根据勾股定理得出方程,求出方程的解即可;
(2)分情况讨论可知,当P点在BF上、Q点在ED上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可.
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵AC的垂直平分线EF,
∴OA=OC,
在△AOE和△COF中,
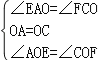 ,
,
∴△AOE≌△COF(ASA),
∴OE=OF,
∵OA=OC,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE是菱形.
∴AF=FC,
设AF=xcm,
则CF=xcm,BF=(8﹣x)cm,
∵四边形ABCD是矩形,
∴∠B=90°,
∴在Rt△ABF中,
由勾股定理得:42+(8﹣x)2=x2,
解得x=5,即AF=5cm;
(2)显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上或P在BF,Q在CD时不构成平行四边形,也不能构成平行四边形.
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t,QA=12﹣4t,
∴5t=12﹣4t,
解得t=![]() .
.
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,t=![]() 秒.
秒.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】2018年五一小长假,杭州市公园、景区共接待游客总量617.57万人次,用科学记数法表示617.57万的结果是( )
A. 6.1757×105 B. 6.1757×106 C. 0.61757×106 D. 0.61757×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏和小聪进行百米赛跑,小敏每秒跑6.3米,小聪每秒跑7.1米,小聪让小敏先跑5米,则比赛结果是( )
A.小敏和小聪同时到达终点
B.小敏比小聪早近1秒到达终点
C.小敏比小聪晩近1秒到达终点
D.小敏比小聪晩近0.9秒到达终点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲校女生占全校总人数的50%,乙校男生占全校总人数的50%,比较两校女生人数( )
A. 甲校女生人数多 B. 乙校女生人数多
C. 甲校与乙校女生人数一样多 D. 以上说法都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省市先后出台了居民用电“阶梯价格”制度,下表是某市的电价标准(每月).
阶梯 | 一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
一档 | 0<x≤180 | a |
二档 | 180<x≤280 | b |
三档 | x>280 | 0.82 |
(1)已知小华家四月份用电200度,缴纳电费105元;五月份用电230度,缴纳电费122.1元,请你根据以上数据,求出表格中a,b的值;
(2)六月份是用电高峰期,小华家计划六月份电费支出不超过208元,那么小华家六月份最多可用电多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com