
【题目】如图,点P是等边△ABC内一点,PA=6,PB=8,PC=10,则△APC的面积是__________

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
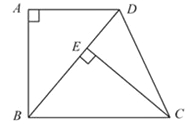
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x﹣1,它的相关函数为 .
.
(1)已知点A(﹣5,8)在一次函数y=ax﹣3的相关函数的图象上,求a的值;
(2)已知二次函数![]() .
.
①当点B(m, ![]() )在这个函数的相关函数的图象上时,求m的值;
)在这个函数的相关函数的图象上时,求m的值;
②当﹣3≤x≤3时,求函数![]() 的相关函数的最大值和最小值;
的相关函数的最大值和最小值;
(3)在平面直角坐标系中,点M,N的坐标分别为(﹣![]() ,1),(
,1),(![]() ,1}),连结MN.直接写出线段MN与二次函数
,1}),连结MN.直接写出线段MN与二次函数![]() 的相关函数的图象有两个公共点时n的取值范围.
的相关函数的图象有两个公共点时n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°

(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?

(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB的解析式为![]() ,且与
,且与![]() 轴交于点A,于y轴交于点B,过点A作直线AB的垂线交y轴于点
轴交于点A,于y轴交于点B,过点A作直线AB的垂线交y轴于点![]() ,过点
,过点![]() 作x轴的平行线交AB于点
作x轴的平行线交AB于点![]() ,再过点
,再过点![]() 作直线AB的垂线交y轴于点
作直线AB的垂线交y轴于点![]() …,按此作法继续下去,则点B1的坐标为_______,A1009的坐标为______.
…,按此作法继续下去,则点B1的坐标为_______,A1009的坐标为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com