
【题目】已知:在Rt△ABC中,AB⊥BC,点O是AC的中点,连接OB,过C点作CD⊥OB,交BO的延长线于垂足D,BC=8,sinα=![]() .
.![]()
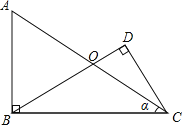
求:(1)线段OC的长;
(2)cos∠DOC的值.
【答案】(1)5;(2)![]()
【解析】
(1)由sinα=![]() =
=![]() ,设AB=3x,则AC=5x,由勾股定理得出方程(3x)2+82=(5x)2,解方程得出AC=10,即可求出OC=
,设AB=3x,则AC=5x,由勾股定理得出方程(3x)2+82=(5x)2,解方程得出AC=10,即可求出OC=![]() AC=
AC=![]() ×10=5;
×10=5;
(2)由直角三角形斜边上的中线性质得出OB=OC=OA=![]() AC=5,设OD=y,则BD=OB+OD=5+y,由勾股定理得出方程82﹣(5+y)2=52﹣y2,得出y=
AC=5,设OD=y,则BD=OB+OD=5+y,由勾股定理得出方程82﹣(5+y)2=52﹣y2,得出y=![]() ,由三角函数定义即可得出答案.
,由三角函数定义即可得出答案.
(1)∵在Rt△ABC中,AB⊥BC,
∴sinα=![]() =
=![]() ,
,
设AB=3x,则AC=5x,
∵AB2+BC2=AC2,
即(3x)2+82=(5x)2,
解得:x1=2,x2=﹣2(不合题意舍去),
∴AC=10,
∵点O是AC的中点,
∴OC=![]() AC=
AC=![]() ×10=5;
×10=5;
(2)∵在Rt△ABC中,AB⊥BC,点O是AC的中点,
∴OB=OC=OA=![]() AC=5,
AC=5,
设OD=y,则BD=OB+OD=5+y,
∵CD⊥OB,
∴CD2=BC2﹣BD2=OC2﹣OD2,
∴82﹣(5+y)2=52﹣y2,
解得:y=![]() ,
,
∴cos∠DOC=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
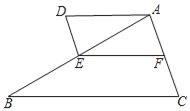
【题目】如图,已知点D在△ABC的外部,AD∥BC,点E在边AB上,ABAD=BCAE.
(1)求证:∠BAC=∠AED;
(2)在边AC取一点F,如果∠AFE=∠D,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2020比佛利”无锡马拉松赛将于3月22日鸣枪开跑,本次比赛设三个项目:A.全程马拉松;B.半程马拉松;C.迷你马拉松.小明和小红都报名参与该赛事的志愿者服务工作,若两人都已被选中,届时组委会随机将他们分配到三个项目组.
(1)小明被分配到“迷你马拉松”项目组的概率为 ;
(2)请利用树状图或列表法求两人被分配到同一个项目组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
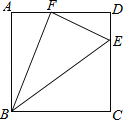
【题目】如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若sin∠DFE=![]() ,则tan∠EBC的值为( )
,则tan∠EBC的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
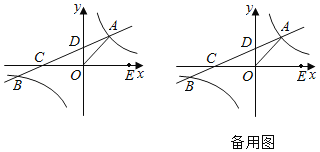
【题目】如图,在平面直角坐标系xOy中,双曲线y=![]() (k≠0)与直线y=ax+b(a≠0)交于A,B两点,直线AB分别交x轴,y轴于C、D两点,若OA=OC,A点坐标为(4,3).
(k≠0)与直线y=ax+b(a≠0)交于A,B两点,直线AB分别交x轴,y轴于C、D两点,若OA=OC,A点坐标为(4,3).
(1)分别求出双曲线与直线的函数表达式;
(2)若P为双曲线上一点,且横坐标为2,H为直线AB上一点,且PH+![]() HC最小,延长PH交x轴于点E,将线段OE沿x轴平移得线段O'E',在平移过程中,是否存在某个位置使|BO'﹣AE'|的值最大值,求出最大值并求出此时E点坐标.
HC最小,延长PH交x轴于点E,将线段OE沿x轴平移得线段O'E',在平移过程中,是否存在某个位置使|BO'﹣AE'|的值最大值,求出最大值并求出此时E点坐标.
(3)在(2)的情况下,将直线OA沿线段CE平移,平移过程中交y=![]() (x>0)的图象于M(M与点A不重合)交x轴于点N,在平面内找一点G,使M、N,E,G为顶点的四边形为矩形?直接写出G的坐标.
(x>0)的图象于M(M与点A不重合)交x轴于点N,在平面内找一点G,使M、N,E,G为顶点的四边形为矩形?直接写出G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。
(1)将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
![]() 求出每天的销售利润
求出每天的销售利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
![]() 如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?
如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?![]() 每天的总成本
每天的总成本![]() 每件的成本
每件的成本![]() 每天的销售量
每天的销售量![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,(k为常数,k≠1).
,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com