(2004•黄冈)在直角坐标系XOY中,O为坐标原点,A,B,C三点的坐标分别为A(5,0),B(0,4),C(-1,0).点M和点N在x轴上(点M在点N的左边),点N在原点的右边,作MP⊥BN,垂足为P(点P在线段BN上,且点P与点B不重合),直线MP与y轴相交于点G,MG=BN.
(1)求经过A,B,C三点的抛物线的表达式;
(2)求点M的坐标;
(3)设ON=t,△MOG的面积为S,求S与t的函数关系式,并写出自变量t的取值范围;
(4)过点B作直线BK平行于x轴,在直线BK上是否存在点R,使△ORA为等腰三角形?若存在,请直接写出点R的坐标,若不存在,请说明理由.
【答案】
分析:(1)已知了A、B、C的坐标,可用待定系数法求出抛物线的解析式;
(2)由于M点的位置不确定,因此可分两种情况:
①M在x轴负半轴,可通过证△BON≌△MOG,得出OM=OB,据此可求出M点的坐标.
②M在x轴正半轴,同①;
(3)根据②的全等三角形可得出ON=OG=t,而OM=4,可根据三角形的面积公式得出关于S,t的函数关系式;
(4)存在5个符合条件的R点,如图:
 解答:
解答:解:(1)设所求抛物线的表达式为:y=ax
2+bx+c(a≠0)
由题意,得

解得
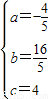
所以所求的表达式为y=-

x
2+

x+4;
(2)依题意,分两种情况:
①当点M在原点的左边(如图1)时,
在Rt△BON中,∠1+∠3=90°
因为MP⊥PN,所以∠2+∠3=90°,
所以∠1=∠2
在Rt△BON和Rt△MOG中,
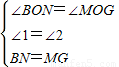
所以Rt△BON≌Rt△MOG
所以OM=OB=4.所以M点的坐标为(-4,0);
②当点M在原点的右边(如图2)时,同理可证OM=OB=4.此时M点的坐标为(4,0).


(3)图1中,Rt△BON≌Rt△MOG,所以OG=ON=t.
所以S=

OM•OG=

•4•t=2t(其中0<t<4).
图2中,同理可得S=2t,其中t>4.
所以所求的函数关系式为S=2t,
t的取值范围为t>0且t≠4;
(4)存在点R,使△ORA为等腰三角形,
其坐标为:R
1(-3,4),R
2(3,4),R
3(2,4),R
4(

,4),R
5(8,4).
点评:本题着重考查了待定系数法求二次函数解析式、三角形全等、等腰三角形的构成等重要知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.



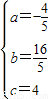
 x2+
x2+ x+4;
x+4;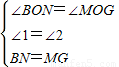


 OM•OG=
OM•OG= •4•t=2t(其中0<t<4).
•4•t=2t(其中0<t<4). ,4),R5(8,4).
,4),R5(8,4).

 黄冈创优卷系列答案
黄冈创优卷系列答案