
【题目】如图,一次函数y=kx+b的图象与反比例函数y=﹣![]() 的图象交于A、B两点,A的横坐标和点B的纵坐标都是﹣2.求:
的图象交于A、B两点,A的横坐标和点B的纵坐标都是﹣2.求:
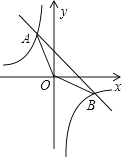
(1)一次函数的表达式;
(2)△AOB的面积;
(3)根据图象,当x在什么范围内时,一次函数的值大于反比例函数的值?
【答案】(1)y=﹣x+2;(2)6;(3)x<﹣2和0<x<4.
【解析】
试题分析:(1)由反比例函数解析式可分别求得A、B两点的坐标,再利用待定系数法可求得一次函数表达式;
(2)设直线一次函数与y轴交于C点,可求得C点坐标,再利用三角形的面积公式计算即可;
(2)一次函数的值大于反比例函数的值时即一次函数的图象在反比例函数图象的上方,结合图象可求得x的范围.
解:
(1)反比例函数y=﹣![]() 的图象交于A、B两点,且A的横坐标和点B的纵坐标都是﹣2,
的图象交于A、B两点,且A的横坐标和点B的纵坐标都是﹣2,
∴A点的纵坐标为和B点的横坐标都为4,
∴A(﹣2,4),B(4,﹣2),
∵一次函数y=kx+b的图象过A、B两点,
∴把A、B两点坐标代入可得![]() ,解得
,解得![]() ,
,
∴一次函数表达式为y=﹣x+2;
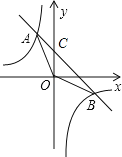
(2)如图,设一次函数与y轴交于点C,则C点坐标为(0,2),
∴OC=2,
∴S△AOB=S△AOC+S△BOC=![]() OC2+
OC2+![]() OC4=6;
OC4=6;
(3)结合图象可知一次函数的图象在反比例函数图象的上方时,对应的x的取值范围为x<﹣2和0<x<4,
∴一次函数的值大于反比例函数的值时对应的x的取值范围为x<﹣2和0<x<4.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形
②以![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形
③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形
其中所有正确结论的序号为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,已知AD=10,CD=4,B′D=2.
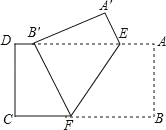
(1)求证:B′E=BF;
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题:
一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.
(2)小明家距小彬家多远?
(3)货车一共行驶了多少千米?
(4)货车每千米耗油0.2升,这次共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小米是一个爱动脑筋的孩子,他用如下方法作∠AOB的角平分线: 作法:如图,
⑴在射线OA上任取一点C,过点C作CD∥OB;
⑵以点C为圆心,CO的长为半径作弧,交CD于点E;
⑶作射线OE.
所以射线OE就是∠AOB的角平分线.请回答:小米的作图依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD平分∠ABC交AC于D,EF垂直平分BD,分别交AB,BC,BD于E,F,G,连接DE,DF. 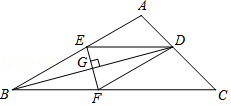
(1)求证:DE=DF;
(2)若∠ABC=30°,∠C=45°,DE=4,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,过点(x1 , 0),﹣3<x1<﹣2,对称轴为直线x=﹣1.给出四个结论:①abc>0;②2a+b=0;③b2>4ac;④3b+2c>0,其中正确的结论有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com