
【题目】如图,在△ABC中,M、N分别是BC与EF的中点,CF⊥AB,BE⊥AC.
(1)求证:MN⊥EF;
(2)连接FM、EM,若![]() ,试判断△FEM的形状.
,试判断△FEM的形状.

【答案】(1)证明见解析;(2)△FEM是等边三角形.
【解析】
(1)连接ME、MF,根据直角三角形斜边上的中线等于斜边的一半可得MF=ME=![]() BC,再根据等腰三角形三线合一的性质证明即可;
BC,再根据等腰三角形三线合一的性质证明即可;
(2)根据等腰三角形两底角相等求出∠BMF+∠CME,然后求出∠EMF=60°,再根据等边三角形的判定方法解答即可.
(1)如图,连接MF、ME.
∵MF、ME分别为Rt△FBC是和Rt△EBC斜边上的中线,∴MF=ME=![]() BC.
BC.
在△MEF中,∵MF=ME,点N是EF的中点,∴MN⊥EF.

(2)∵ME=MF=BM=CM,∴∠MBA=∠MFB,∠MEC=∠MCE,∴∠BMF+∠CME=180°﹣2∠ABC+180°﹣2∠ACB=360°﹣2(∠ABC+∠ACB).
∵∠A=60°,∴∠ABC+∠ACB=180°﹣60°=120°,∴∠BMF+∠CME=360°﹣2×120°=120°,∴∠EMF=60°,∴△MFE是等边三角形.


科目:初中数学 来源: 题型:
【题目】当n为1,2,3,…时,由大小相同的小正方形组成的图形如图所示,则第10个图形中小正方形的个数总和等于( )
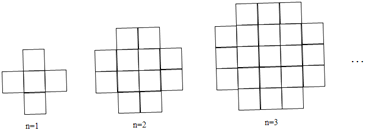
A. 100 B. 96 C. 144 D. 140
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班共有50名学生,在某次活动中被分为四组,第一组有a人,第二组的人数比第一组人数的一半多6人,第三组的人数等于前两组人数的和.
(1)求第四组的人数;(用含a的式子表示)
(2)试判断当a=14时,是否满足题意.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上的一点,点E在BC边上,连接AE,DE,DC,AE=CD.
(1)求证:△ABE≌△CBD;
(2)若∠BAE=15°,求∠EDC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)自2014年12月启动“绿茵行动,青春聚力”郴州共青林植树活动以来,某单位筹集7000元购买了桂花树和樱花树共30棵,其中购买桂花树花费3000元.已知桂花树比樱花树的单价高50%,求樱花树的单价及棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已抢修道路 米;
时,已抢修道路 米;
(2)求原计划每小时抢修道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,点B是数轴上原点O两侧的两点,其中点A在负半轴上,且满足AB=12,OB=2OA.
(1)点A,B在数轴上对应的数分别为 和 ;
(2)点A,B同时分别以每秒2个单位长度和每秒4个单位长度的速度向左运动.
①经过几秒后,OA=3OB;
②点A,B在运动的同时,点P以每秒2个单位长度的速度从原点向右运动,经过几秒后,点A,B,P中的某一点成为其余两点所连线段的中点.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com