
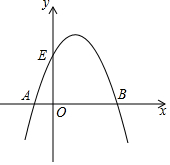
 已知抛物线经过点A(-1,0),B(3,0),C(1,4),与y轴交于点E.
已知抛物线经过点A(-1,0),B(3,0),C(1,4),与y轴交于点E.分析 (1)设抛物线解析式y=ax2+bx+c,把点A(-1,0),B(3,0),C(1,4),分别代入求出a,b,c的值即可求出抛物线的解析式;
(2)设x轴上有一点G,使得S△EGB=15,易求点G的坐标,过点G作GF∥BE,交第三象限抛物线于点F,求出直线GF解析式,即可求出点F的坐标;
(3)分点P在点Q的左边和右边两种情况,根据平行四边形的对边平行且相等,从点A、C的坐标关系,用点P的坐标表示出点Q的坐标,然后把点Q的坐标代入抛物线解析式求解即可.
解答 解:
(1)设抛物线解析式y=ax2+bx+c,把点A(-1,0),B(3,0),C(1,4)代入得:
$\left\{\begin{array}{l}{0=a-b+c}\\{0=9a+3b+c}\\{4=16a+4b+c}\end{array}\right.$,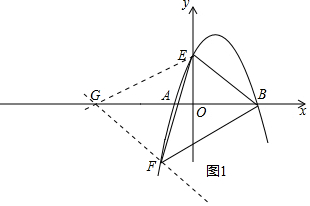
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式是y=-x2+2x+3;
(2)设x轴上有一点G,使得S△EGB=15,
∵EO=3,
∴BG=10,
∵BO=3,
∴OG=7,
∴点G坐标是(-7,0),
过G作GF∥BE,交第三象限抛物线于点F,
设直线BE的解析式为y=kx+b,
由点B(3,0),点E坐标(0,3)可得y=-x-3,
∴直线GF解析式为y=-x-7,
联立抛物线和直线GF的解析式得:$\left\{\begin{array}{l}{y=-{x}^{2}+2x+3}\\{y=-x-7}\end{array}\right.$,
解得:x=-2,y=-5或x=5,y=12,
∵点F在第三象限的抛物线上,
∴点F的坐标是(-2,-5);
(3)∵直线l∥AC,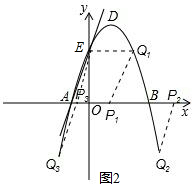
∴PQ∥AC且PQ=AC,
∵A(-1,0),C(0,3),
∴设点P的坐标为(x,0),
则①若点Q在x轴上方,则点Q的坐标为(x+1,3),
此时,-(x+1)2+2(x+1)+3=3,
解得x1=-1(舍去),x2=1,
所以,点Q的坐标为(2,3),
②若点Q在x轴下方,则点Q的坐标为(x-1,-3),
此时,-(x-1)2+2(x-1)+3=-3,
整理得,x2-4x-3=0,
解得x1=2+$\sqrt{7}$,x2=2-$\sqrt{7}$,
所以,点Q的坐标为(1+$\sqrt{7}$,-3)或(1-$\sqrt{7}$,-3),
综上所述,点Q的坐标为(2,3)或(1+$\sqrt{7}$,-3)或(1-$\sqrt{7}$,-3).
点评 本题是二次函数综合题型,主要考查了抛物线与x轴的交点问题,待定系数法求二次函数解析式,平行四边形的对边平行且相等的性质,(2)确定出点F的位置是解题的关键,(3)难点在于分情况讨论.


科目:初中数学 来源: 题型:解答题
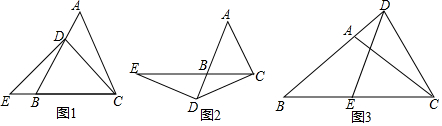
 已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,过点B作BK⊥AC,垂足为K,过D作DH∥KB,DH分别与AC,AB,⊙O及CB的延长线相交于点E,F,G,H,且F是EG的中点.
已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,过点B作BK⊥AC,垂足为K,过D作DH∥KB,DH分别与AC,AB,⊙O及CB的延长线相交于点E,F,G,H,且F是EG的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
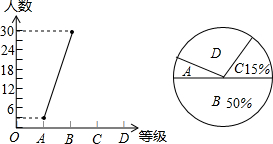 为迎接常熟市文明城市创建工作,某校八年级一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动,成绩分为A、B、C、D四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:
为迎接常熟市文明城市创建工作,某校八年级一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动,成绩分为A、B、C、D四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在5×5的正方形网格中,每个小正方形的边长为1,用四边形覆盖如图所示,被覆盖的网格线中,竖直部分的线段的长度之和记作m,水平部分的线段的长度之和记作n,则m-n=( )
在5×5的正方形网格中,每个小正方形的边长为1,用四边形覆盖如图所示,被覆盖的网格线中,竖直部分的线段的长度之和记作m,水平部分的线段的长度之和记作n,则m-n=( )| A. | 0 | B. | 0.5 | C. | -0.5 | D. | 0.75 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
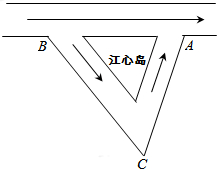 如图,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后,又继续顺流航行2.5小时到达C点,总共行驶了208千米,已知游艇在静水中的速度是38千米/小时.
如图,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后,又继续顺流航行2.5小时到达C点,总共行驶了208千米,已知游艇在静水中的速度是38千米/小时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com