
【题目】一个圆形喷水池的中心竖立一根高为![]() 顶端装有喷头的水管,喷头喷出的水柱呈抛物线形.当水柱与池中心的水平距离为
顶端装有喷头的水管,喷头喷出的水柱呈抛物线形.当水柱与池中心的水平距离为![]() 时,水柱达到最高处,高度为
时,水柱达到最高处,高度为![]() .
.
![]() 求水柱落地处与池中心的距离;
求水柱落地处与池中心的距离;
![]() 如果要将水柱的最大高度再增加
如果要将水柱的最大高度再增加![]() ,水柱的最高处与池中心的水平距离以及落地处与池中心的距离仍保持不变,那么水管的高度应是多少?
,水柱的最高处与池中心的水平距离以及落地处与池中心的距离仍保持不变,那么水管的高度应是多少?
【答案】![]() 水柱落地处与池中心的距离为
水柱落地处与池中心的距离为![]() ;
;![]() 水管的高度应为
水管的高度应为![]() .
.
【解析】
首先根据题意建立直角坐标系,画出拋物线、(1)结合图形我们可以知道此拋物线的顶点坐标(1,3),而且抛物线经过点(0,2.25),求出抛物线的解析式,把(x,0)代入解析式即可解题,
(2)由(1)的结论我们知道了水柱落地的坐标为(3,0),顶点坐标为(1,4),求出新的拋物线的解析式,再求水管的高度即可解题.
![]() 如图,建立直角坐标系,点
如图,建立直角坐标系,点![]() 是抛物线的顶点.
是抛物线的顶点.
由题意,设水柱所在的抛物线的解析式为![]() ,
,
∵抛物线经过点![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
当![]() 时,即
时,即![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
即水柱落地处与池中心的距离为![]() ;
;

![]() 由题意,设抛物线解析式为
由题意,设抛物线解析式为![]() ,
,
∵抛物线经过点![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
即水管的高度应为![]() .
.


科目:初中数学 来源: 题型:
【题目】四位同学在研究函数y=x2+bx+c(b,c是常数)时,甲发现当x=1时,函数有最小值;乙发现﹣1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,E是CD延长线上的一点,BE与AD交于点F,DE=![]() CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知二次函数![]() .
.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
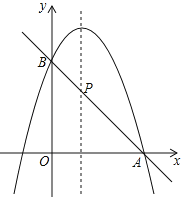
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
小聪观察上表,得出下面结论:①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ;②函数
;②函数![]() 的最大值为
的最大值为![]() ;③抛物线的对称轴是
;③抛物线的对称轴是![]() ;④在对称轴左侧,
;④在对称轴左侧,![]() 随
随![]() 增大而增大.其中正确有( )
增大而增大.其中正确有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园有![]() 棵枇杷树.每棵平均产量为
棵枇杷树.每棵平均产量为![]() 千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵树接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量
千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵树接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量![]() 千克,若设增种
千克,若设增种![]() 棵枇杷树,投产后果园枇杷的总产量为
棵枇杷树,投产后果园枇杷的总产量为![]() 千克,则
千克,则![]() 与
与![]() 之间的函数关系式为________.
之间的函数关系式为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(-2,3),B(-3,2),C(-1,1).

(1)若将△ABC向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的△A1B1C1;
(2)画出△A1B1C1绕原点旋转180°后得到的△A2B2C2;
(3)△A'B'C'与△ABC是位似图形,请写出位似中心的坐标:______;
(4)顺次连接C,C1,C',C2,所得到的图形是轴对称图形吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=ax2+(![]() ﹣2a)x(a<0),下列说法正确的个数是( )
﹣2a)x(a<0),下列说法正确的个数是( )
①对于任何满足条件的a,该二次函数的图象都经过点(2,1)和(0,0)两点;
②若该函数图象的对称轴为直线x=x0,则必有1<x0<2;
③当x≥0时,y随x的增大而增大;
④若P(4,y1),Q(4+m,y2)(m>0)是函数图象上的两点,如果y1>y2总成立,则a≤﹣![]() .
.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com