
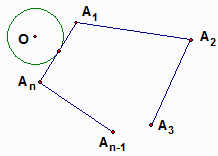
 6、如图,⊙O沿凸多边形A1A2A3…An-1An的外侧(圆与边相切)作无滑动的滚动.假设⊙O的周长是凸多边形A1A2A3…An-1An的周长的一半,那么当⊙O回到出发点时,它自身滚动的圈数为( )
6、如图,⊙O沿凸多边形A1A2A3…An-1An的外侧(圆与边相切)作无滑动的滚动.假设⊙O的周长是凸多边形A1A2A3…An-1An的周长的一半,那么当⊙O回到出发点时,它自身滚动的圈数为( ) 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
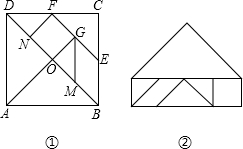 对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
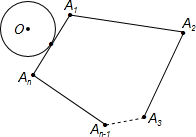 如图,⊙O沿凸多边形A1A2A3…An-1An的外侧(圆与边相切)作无滑动的滚动.假设⊙O的周长是凸多边形A1A2A3…An-1An的周长的一半,那么当⊙O回到出发点时,它自身滚动的圈数为
如图,⊙O沿凸多边形A1A2A3…An-1An的外侧(圆与边相切)作无滑动的滚动.假设⊙O的周长是凸多边形A1A2A3…An-1An的周长的一半,那么当⊙O回到出发点时,它自身滚动的圈数为查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
查看答案和解析>>
科目:初中数学 来源:2008年第4届“锐丰杯”初中数学邀请赛试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com