
【题目】如图,抛物线y=ax2+bx﹣4经过A(﹣3,0),B(5,﹣4)两点,与y轴交于点C,连接AB,AC,BC.
(1)求抛物线的表达式;
(2)求△ABC的面积;
(3)抛物线的对称轴上是否存在点M,使得△ABM是直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣4;(2)10;(3)存在,M1(
x﹣4;(2)10;(3)存在,M1(![]() ,11),M2(
,11),M2(![]() ,﹣
,﹣![]() ),M3(
),M3(![]() ,
,![]() ﹣2),M4(
﹣2),M4(![]() ,﹣
,﹣![]() ﹣2).
﹣2).
【解析】
(1)将点A,B代入y=ax2+bx﹣4即可求出抛物线解析式;
(2)在抛物线y=![]() x2﹣
x2﹣![]() x﹣4中,求出点C的坐标,推出BC∥x轴,即可由三角形的面积公式求出△ABC的面积;
x﹣4中,求出点C的坐标,推出BC∥x轴,即可由三角形的面积公式求出△ABC的面积;
(3)求出抛物线y=![]() x2﹣
x2﹣![]() x﹣4的对称轴,然后设点M(
x﹣4的对称轴,然后设点M(![]() ,m),分别使∠AMB=90°,∠ABM=90°,∠AMB=90°三种情况进行讨论,由相似三角形和勾股定理即可求出点M的坐标.
,m),分别使∠AMB=90°,∠ABM=90°,∠AMB=90°三种情况进行讨论,由相似三角形和勾股定理即可求出点M的坐标.
解:(1)将点A(﹣3,0),B(5,﹣4)代入y=ax2+bx﹣4,
得![]() ,
,
解得,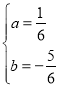 ,
,
∴抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣4;
x﹣4;
(2)在抛物线y=![]() x2﹣
x2﹣![]() x﹣4中,
x﹣4中,
当x=0时,y=﹣4,
∴C(0,﹣4),
∵B(5,﹣4),
∴BC∥x轴,
∴S△ABC=![]() BCOC
BCOC
=![]() ×5×4
×5×4
=10,
∴△ABC的面积为10;
(3)存在,理由如下:
在抛物线y=![]() x2﹣
x2﹣![]() x﹣4中,
x﹣4中,
对称轴为:![]() ,
,
设点M(![]() ,m),
,m),
①如图1,
当∠M1AB=90°时,
设x轴与对称轴交于点H,过点B作BN⊥x轴于点N,
则HM1=m,AH=![]() ,AN=8,BN=4,
,AN=8,BN=4,
∵∠AM1H+∠M1AN=90°,∠M1AN+∠BAN=90°,
∴∠M1AH=∠BAN,
又∵∠AHM1=∠BNA=90°,
∴△AHM1∽△BNA,
∴![]() ,
,
即![]() ,
,
解得,m=11,
∴M1(![]() ,11);
,11);
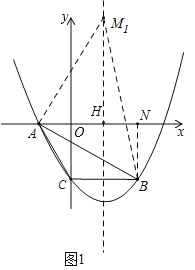
②如图2,
当∠ABM2=90°时,
设x轴与对称轴交于点H,BC与对称轴交于点N,
由抛物线的对称性可知,对称轴垂直平分BC,
∴M2C=M2B,
∴∠BM2N=∠AM2N,
又∵∠AHM2=∠BNM2=90°,
∴△AHM2∽△BNM2,
∴![]() ,
,
∵HM2=﹣m,AH=![]() ,BN=
,BN=![]() ,M2N=﹣4﹣m,
,M2N=﹣4﹣m,
∴ ,
,
解得,![]() ,
,
∴M2(![]() ,﹣
,﹣![]() );
);
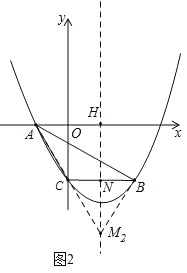
③如图3,
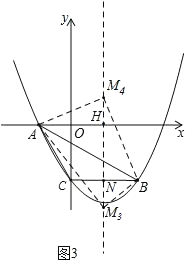
当∠AMB=90°时,
设x轴与对称轴交于点H,BC与对称轴交于点N,
则AM2+BM2=AB2,
∵AM2=AH2+MH2,BM2=BN2+MN2,
∴AH2+MH2+BN2+MN2=AB2,
∵HM=﹣m,AH=![]() ,BN=
,BN=![]() ,MN=﹣4﹣m,
,MN=﹣4﹣m,
即![]() ,
,
解得,m1=![]() ﹣2,m2=﹣
﹣2,m2=﹣![]() ﹣2,
﹣2,
∴M3(![]() ,
,![]() ﹣2),M4(
﹣2),M4(![]() ,﹣
,﹣![]() ﹣2);
﹣2);
综上所述,存在点M的坐标,其坐标为M1(![]() ,11),M2(
,11),M2(![]() ,﹣
,﹣![]() ),M3(
),M3(![]() ,
,![]() ﹣2),M4(
﹣2),M4(![]() ,﹣
,﹣![]() ﹣2).
﹣2).


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
【题目】用铁片制作的圆锥形容器盖如图所示.
(1)我们知道:把平面内线段OP绕着端点O旋转1周,端点P运动所形成的图形叫做圆.类比圆的定义,给圆锥下定义 ;
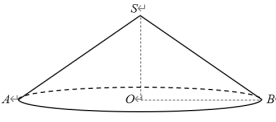
(2)已知OB=2 cm,SB=3 cm,
①计算容器盖铁皮的面积;
②在一张矩形铁片上剪下一个扇形,用它围成该圆锥形容器盖.以下是可供选用的矩形铁片的长和宽,其中可以选择且面积最小的矩形铁片是 .
A.6 cm×4 cm B.6 cm×4.5 cm C.7 cm×4 cm D.7 cm×4.5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在正方形ABCD中,AD=4,E,F分别是CD,BC上的一点,且∠EAF=45°,EC=1,将△ADE绕点A沿顺时针方向旋转90°后与△ABG重合,连接EF,过点B作BM∥AG,交AF于点M,则以下结论:①DE+BF=EF,②BF=![]() ,③AF=
,③AF=![]() ,④S△MEF=
,④S△MEF=![]() 中正确的是
中正确的是![]()
![]()
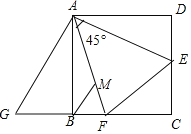
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=![]() (k≠0,x>0)过点D.
(k≠0,x>0)过点D.
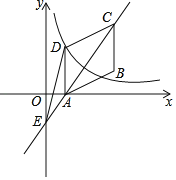
(1)写出D点坐标;
(2)求双曲线的解析式;
(3)作直线AC交y轴于点E,连结DE,求△CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②b2﹣4ac>0;③9a﹣3b+c>0;④b﹣4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=﹣4,其中正确的结论有( )
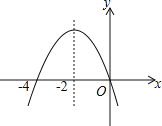
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,按下列步骤作图:①以点A为圆心,适当长为半径画弧,分别交AC,AB于点D,E;②分别以D,E为圆心,DE的长为半径画弧,两弧相交于点F;③作射线AF,交BC于点G,则CG=( )
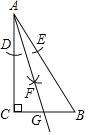
A.3B.6C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校有一栋教学楼AB,小明(身高忽略不计)在教学楼一侧的斜坡底端C处测得教学楼顶端A的仰角为68°,他沿着斜坡向上行走到达斜坡顶端E处,又测得教学楼顶端A的仰角为45°.已知斜坡的坡角(∠ECD)为30°,坡面长度CE=6m,求楼房AB的高度.(结果精确到0.1m,参考数据:tan68°≈2.48,![]() ≈1.73)
≈1.73)
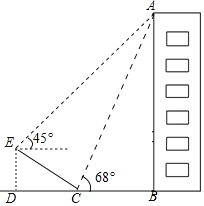
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数和等于0?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小辉和小乐一起在学校寄宿三年了,毕业之际,他们想合理分配共同拥有的三件“财产”:一个电子词典、一台迷你唱机、一套珍藏版小说.他们本着“在尊重各自的价值偏好基础上进行等值均分”的原则,设计了分配方案,步骤如下(相应的数额如表二所示):
①每人各自定出每件物品在心中所估计的价值;
②计算每人所有物品估价总值和均分值(均分:按总人数均分各自估价总值);
③每件物品归估价较高者所有;
④计算差额(差额:每人所得物品的估价总值与均分值之差);
⑤小乐拿225元给小辉,仍“剩下”的300元每人均分.
依此方案,两人分配的结果是:小辉拿到了珍藏版小说和375元钱,小乐拿到的电子词典和迷你唱机,但要付出375元钱.
(1)甲、乙、丙三人分配A,B,C三件物品,三人的估价如表三所示,依照上述方案,请直接写出分配结果;
(2)小红和小丽分配D,E两件物品,两人的估价如表四所示(其中0<m-n<15).按照上述方案的前四步操作后,接下来,依据“在尊重各自的价值偏好基础上进行等值均分”的原则,该怎么分配较为合理?请完成表四,并写出分配结果.(说明:本题表格中的数值的单位均为“元”)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com