
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点E在边AB上,点F是边BC上不与点B、C重合的一个动点,把
,点E在边AB上,点F是边BC上不与点B、C重合的一个动点,把![]() 沿EF折叠,点B落在点
沿EF折叠,点B落在点![]() 处.若
处.若![]() ,当
,当![]() 是以
是以![]() 为腰的等腰三角形时,线段
为腰的等腰三角形时,线段![]() 的长为__________.
的长为__________.

【答案】16或10
【解析】
等腰三角形一般分情况讨论:(1)当DB'=DC=16;(2)当B'D=B'C时,作辅助线,构建平行四边形AGHD和直角三角形EGB',计算EG和B'G的长,根据勾股定理可得B'D的长;
∵四边形ABCD是矩形,
∴DC=AB=16,AD=BC=18.
分两种情况讨论:
(1)如图2,当DB'=DC=16时,即△CDB'是以DB'为腰的等腰三角形
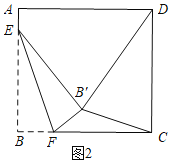
(2)如图3,当B'D=B'C时,过点B'作GH∥AD,分别交AB与CD于点G、H.

∵四边形ABCD是矩形,
∴AB∥CD,∠A=90°
又GH∥AD,
∴四边形AGHD是平行四边形,又∠A=90°,
∴四边形AGHD是矩形,
∴AG=DH,∠GHD=90°,即B'H⊥CD,
又B'D=B'C,
∴DH=HC=![]() ,AG=DH=8,
,AG=DH=8,
∵AE=3,
∴BE=EB'=AB-AE=16-3=13,
EG=AG-AE=8-3=5,
在Rt△EGB'中,由勾股定理得:
GB′=![]() ,
,
∴B'H=GH×GB'=18-12=6,
在Rt△B'HD中,由勾股定理得:B′D=![]()
综上,DB'的长为16或10.
故答案为: 16或10


科目:初中数学 来源: 题型:
【题目】EF是平行四边ABCD的对角线BD的垂直平分线,EF与边AD,BC分别交于点E,F.

(1)求证:四边形BFDE是菱形;
(2)若ED=5,BD=8,求菱形BFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,商店考虑继续按之前的降价率再次降价,请你算一算第三次降价后出售的商品是否会亏本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() .
.

(1)如图1,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,
,![]() .若
.若![]() ,求线段
,求线段![]() 的长.
的长.
(2)如图2,![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边向上构造等边三角形
为边向上构造等边三角形![]() ,线段
,线段![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.连接
的中点.连接![]() ,
,![]() 判断
判断![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
(3)在(2)的条件下,若![]() ,请你直接写出
,请你直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中,正确的是( )

A. ac<0 B. a+b+c<0 C. b2﹣4ac<0 D. b=8a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)完成下面的证明.
如图,在四边形![]() 中,
中,![]() ,
,![]() 是
是![]() 的平分线.求证:
的平分线.求证:![]() .
.

证明:![]() 是
是![]() 的平分线(已知)
的平分线(已知)
![]() _________
_________![]() _________(角平分线的定义)
_________(角平分线的定义)
又![]() (已知)
(已知)
![]() _________
_________![]() _________(等量代换)
_________(等量代换)
![]() (____________________________)
(____________________________)
(2)已知线段![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 在直线
在直线![]() 上,且
上,且![]() ,画图并计算
,画图并计算![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com