
分析 先化简将1-x2与x-1统一形式,将1-x2化为-(x2-1),再乘以最简公分母(x+1)(x-1),化成整式方程,解出x=1,要把x=1代入最简公分母进行检验,当x=1时,x2-1=0,所以原分式方程无解.
解答 解:$\frac{4}{1-x^2}$=1-$\frac{x+1}{x-1}$,
$\frac{-4}{{x}^{2}-1}$=1-$\frac{x+1}{x-1}$,
去分母,方程两边同时乘以(x+1)(x-1),
-4=x2-1-(x+1)2,
-4=-1-2x-1,
x=1,
当x=1时,x2-1=0,
所以x=1不是原分式方程的解,
所以原分式方程无解.
点评 本题是解分式方程,熟练掌握解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.注意解分式方程必须检验.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
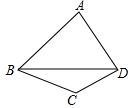 如图四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=128°,则∠A的度数是( )
如图四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=128°,则∠A的度数是( )| A. | 60° | B. | 76° | C. | 77° | D. | 78° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
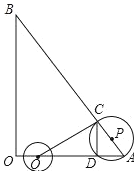 如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 与标准重量偏差(单位:千克) | -2 | -1 | 0 | 1 | 2 | 3 |
| 袋 数 | 5 | 10 | 3 | 1 | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{48}{x+4}+\frac{48}{x-4}=9$ | B. | $\frac{48}{4+x}+\frac{48}{4-x}=9$ | C. | $\frac{48}{(x+4)+(x-4)}=9$ | D. | $\frac{96}{x+4}+\frac{96}{x-4}=9$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com