抛物线y=-x2+2x+3与x轴交于A、B两点(A在B的左侧),与y轴交于点D,顶点为C
(1)求A、B、C、D各点坐标;
(2)求四边形ABCD的面积;
(3)抛物线上是否存在点P,使△PAB的面积是△ABC的面积的2倍?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】
分析:(1)在抛物线的解析式中,当x=0时,可求出点D的坐标;当y=0时,能求出A、B点的坐标;将抛物线的解析式写成顶点式,可以得到顶点C的坐标.
(2)四边形ADCB的形状不规则,可以过C作x轴的垂线,将四边形分成两个直角三角形和一个梯形,根据图形间面积的和差关系求解即可.
(3)由(1)知,抛物线的顶点纵坐标为4,若△PAB的面积是2倍的△ABC的面积,那么点P到x轴的距离必为8(两个三角形共用一个底),显然点P不可能在x轴的上方,所以点P的纵坐标一定是-8,代入抛物线的解析式中求解即可.
解答:解:(1)∵y=-x
2+2x+3=-(x+1)(x-3)=-(x-1)
2+4,
∴A(-1,0)、B(3,0)、C(1,4)、D(0,3).

(2)过C作CE⊥x轴,垂足为E;
由(1)知:OA=1、OD=3、CE=4、OE=1、BE=2;
S
四边形ABCD=S
△AOD+S
△BCE+S
梯形ODCE=

×1×3+

×2×4+

×(3+4)×1=9.
(3)由于CE=4,即点C到x轴的距离为4;
若S
△PAB=2S
△ABC,则点P到x轴的距离为8,
设P(x,-8),依题意,有:
-x
2+2x+3=-8,
化简得:x
2-2x-11=0
解得:x=1±2

;
即:P(1±2

,-8).
点评:此题主要考查了抛物线与坐标轴交点坐标的求法以及图形面积的求法,总体来说难度不大,注意两点即可:图形不规则时,其面积可通过图形间面积和差关系来解;同底不等高的三角形,面积比等于高的比.

 (2)过C作CE⊥x轴,垂足为E;
(2)过C作CE⊥x轴,垂足为E; ×1×3+
×1×3+ ×2×4+
×2×4+ ×(3+4)×1=9.
×(3+4)×1=9. ;
; ,-8).
,-8).

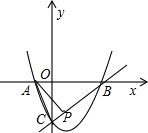 A是抛物线与x轴的另一个交点.
A是抛物线与x轴的另一个交点.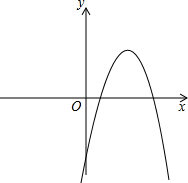 已知一元二次方程-x2+bx+c=0的两个实数根是m,4,其中0<m<4.
已知一元二次方程-x2+bx+c=0的两个实数根是m,4,其中0<m<4.