【题目】平行四边形一定具有的性质是（ ）
A. 四边都相等B. 对角相等C. 对角线相等D. 是轴对称图形
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点． 
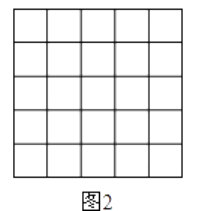
（1）在图1中以格点为顶点画一个面积为10的正方形；
（2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、 
、 
；
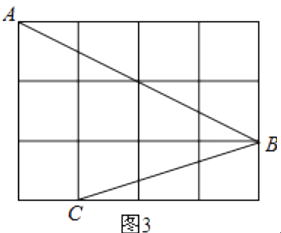
（3）如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
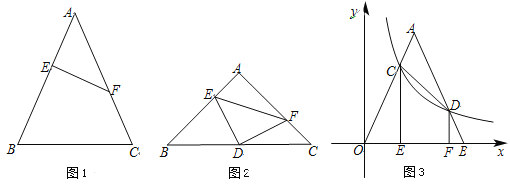
【题目】定义：如图1，等腰△ABC中，点E，F分别在腰AB，AC上，连结EF，若AE＝CF，则称EF为该等腰三角形的逆等线．
（1）如图1，EF是等腰△ABC的逆等线，若EF⊥AB，AB＝AC＝5，AE ＝2，求逆等线EF的长；
（2）如图2，若等腰直角△DEF的直角顶点D恰好为等腰直角△ABC底边BC上的中点，且点E，F分别在AB，AC上，求证：EF为等腰△ABC的逆等线；
（3）如图3，等腰△AOB的顶点O与原点重合，底边OB在x轴上，反比例函数y＝ 
（x＞0）的图象交△OAB于点C，D，若CD恰为△AOB的逆等线，过点C，D分别作CE⊥x轴，DF⊥x轴，已知OE＝2，求OF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
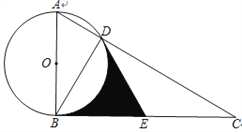
【题目】如图，Rt△ABC中，∠ABC为直角，以AB为直径作⊙O交AC于点D，点E为BC中点，连结DE，DB.
（1）求证：DE与⊙O相切；
（2）若∠C＝30°，求∠BOD的度数；
（3）在（2）的条件下，若⊙O半径为2， 求阴影部分面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我市计划对某地块的1000m2区域进行绿化，由甲、乙两个工程队合作完成．已知甲队每天能完成绿化的面积是乙队的2倍；若两队分别各完成300m2的绿化时，甲队比乙队少用3天．
（1）求甲、乙两工程队每天能完成的绿化的面积；
（2）两队合作完成此工程，若甲队参与施工x天，试用含x的代数式表示乙队施工的天数y；
（3）若甲队每天施工费用是0.6万元，乙队每天为0.2万元，且要求两队施工的天数之和不超过16天，应如何安排甲、乙两队施工的天数，才能使施工总费用最低？并求出最低费用时的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】因式分解与整数乘法一样，都是一种恒等变形，即在变形的过程中，形变值不变，于是将多项式x2﹣y2+（2x+2y）分解因式的结果为（ ）
A.（x+y）（x﹣y+2）
B.（x+y）（x﹣y﹣2）
C.（x﹣y）（x﹣y+2）
D.（x﹣y）（x﹣y﹣2）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为增强学生的身体素质，教育行政部门规定学生每天参加户外活动的平均时间不少于1小时．为了解学生参加户外活动的情况，对部分学生参加户外活动的时间进行抽样调查，并将调查结果绘制作成如下两幅不完整的统计图，请你根据图中提供的信息解答下列问题：
（1）在这次调查中共调查了多少名学生？
（2）求户外活动时间为1.5小时的人数，并补充频数分布直方图；
（3）求表示户外活动时间1小时的扇形圆心角的度数；
（4）本次调查中学生参加户外活动的平均时间是否符合要求？户外活动时间的众数和中位数是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，甲、乙、丙、丁四个长方形拼成正方形EFGH，中间阴影为正方形．已知甲、乙、丙、丁四个长方形面积的和是32cm2 ， 四边形ABCD的面积是20cm2 ， 则甲、乙、丙、丁四个长方形周长的总和为cm．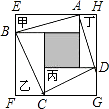 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
