
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D. 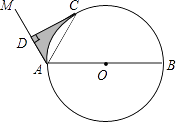
(1)求证:CD是⊙O的切线;
(2)若∠ACD=30°,AD=4,求图中阴影部分的面积.
【答案】
(1)证明:连接OC.
∵OA=OC.
∴∠OAC=∠OCA,
∵∠MAC=∠OAC,
∴∠MAC=∠OCA,
∴OC∥AM,
∵CD⊥AM,
∴OC⊥CD,
∴CD是⊙O的切线

(2)解:在RT△ACD中,∵∠ACD=30°,AD=4,∠ADC=90°,
∴AC=2AD=8,CD= ![]() AD=4
AD=4 ![]() ,
,
∵∠MAC=∠OAC=60°,OA=OC,
∴△AOC是等边三角形,
∴S阴=S△ACD﹣(S扇形OAC﹣S△AOC)
= ![]() ×4×4
×4×4 ![]() ﹣(
﹣( ![]() ﹣
﹣ ![]() ×82)
×82)
=24 ![]() ﹣
﹣ ![]() π
π
【解析】(1)先证明OC∥AM,由CD⊥AM,推出OC⊥CD即可解决问题.(2)根据S阴=S△ACD﹣(S扇形OAC﹣S△AOC)计算即可.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】在开展“好书伴我成长”的读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数.统计数据如下表所示:

(1)求这50个样本数据的平均救,众数和中位数.
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两组卡片共5张,A中三张分别写有数字2,4,6,B中两张分别写有3,5.它们除了数字外没有任何区别.
(1)随机地从A中抽取一张,求抽到数字为2的概率;
(2)随机地分别从A、B中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果,现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
(3)如果不公平请你修改游戏规则使游戏规则对甲乙双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知关于x的方程kx=11﹣2x有整数解,则负整数k的值为 .
(2)若a+b+c=0,且a>b>c,以下结论:
①a>0,c>0;
②关于x的方程ax+b+c=0的解为x=1;
③a2=(b+c)2;
④![]() 的值为0或2;
的值为0或2;
⑤在数轴上点A、B、C表示数a、b、c,若b<0,则线段AB与线段BC的大小关系是AB>BC.
其中正确的结论是 (填写正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 36=15+21 B. 25=9+16 C. 13=3+10 D. 49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.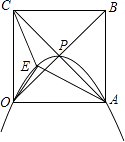
(1)建立适当的平面直角坐标系,
①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:问题:如图1,在菱形ABCD和菱形BEFG中,∠ABC=∠BEF=60°,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC,探究PG与PC的位置关系。
(1)请你写出上面问题中线段PG与PC的位置关系,并说明理由;
(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明,
(3)将菱形ABCD和菱形BEFG均改成正方形,如图3,P为DF的中点,此时PG与PC的位置关系和数量关系分别是什么?直接写出答案。



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个数用大括号围起来,中间用逗号断开,如:{1,2,﹣3}、{﹣2,7,![]() ,19},我们称之为集合,其中的每个数称为该集合的元素.如果一个所有元素均为有理数的集合满足:当有理数a是集合的元素时,2015﹣a也必是这个集合的元素,这样的集合我们称为好的集合.例如集合{2015,0}就是一个好的集合.
,19},我们称之为集合,其中的每个数称为该集合的元素.如果一个所有元素均为有理数的集合满足:当有理数a是集合的元素时,2015﹣a也必是这个集合的元素,这样的集合我们称为好的集合.例如集合{2015,0}就是一个好的集合.
(1)集合{2015}_____好的集合,集合{﹣1,2016}_____好的集合(两空均填“是”或“不是”);
(2)若一个好的集合中最大的一个元素为4011,则该集合是否存在最小的元素?如果存在,请直接写出答案,否则说明理由;
(3)若一个好的集合所有元素之和为整数M,且22161<M<22170,则该集合共有几个元素?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A对应的数为![]() ,点B对应的数为
,点B对应的数为![]() ,且多项式
,且多项式![]() 的二次项系数为
的二次项系数为![]() ,常数项为
,常数项为![]() .
.
(1)直接写出:![]() ;
;
(2)数轴上点A、B之间有一动点P,若点P对应的数为![]() ,试化简
,试化简![]() ;
;
(3)若点M从点A出发,以每秒1个单位长度的速度沿数轴向右移动;同时点N从点B出发,沿数轴每秒2个单位长度的速度向左移动,到达A点后立即返回并向右继续移动,求经过多少秒后,M、N两点相距1个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com