
| A. | 3 | B. | -3 | C. | 3(b-a) | D. | 无法确定 |
分析 设1+a=x,1+b=y,则b-a=y-x,原方程可化为$\frac{1}{x}$-$\frac{1}{y}$=$\frac{1}{y-x}$,整理得,y2-3xy+x2=0,两边同除以x2,求出$\frac{y}{x}$的值,再代入代数式进行计算即可.
解答 解:∵设1+a=x,1+b=y,则b-a=y-x,
∴原式可化为$\frac{1}{x}$-$\frac{1}{y}$=$\frac{1}{y-x}$,整理得y2-3xy+x2=0,两边同除以x2得$\frac{y}{x}$=$\frac{3±\sqrt{5}}{2}$,
∴$\frac{1+b}{1+a}$=$\frac{3±\sqrt{5}}{2}$,
∴$\frac{1+b}{1+a}$-$\frac{1+a}{1+b}$=$\frac{3±\sqrt{5}}{2}$-$\frac{2}{3±\sqrt{5}}$=3.
故选A.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某建筑工程队,在工地一边的靠墙处,用120米长的铁栅栏围成一个所占面积为长方形的临时仓库,已知墙的长度为60米,铁栅栏只围三边,如图所示,设所围成的长方形的面积为1600平方米,求长方形的宽x为多少米?
某建筑工程队,在工地一边的靠墙处,用120米长的铁栅栏围成一个所占面积为长方形的临时仓库,已知墙的长度为60米,铁栅栏只围三边,如图所示,设所围成的长方形的面积为1600平方米,求长方形的宽x为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
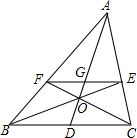 如图,已知△ABC,点E在边AC上,点F在边AB上,EF∥BC,BE与CF交于点O,连接AO交EF于点G,延长AO交BC于点D,求证:BD=CD,EG=FG.
如图,已知△ABC,点E在边AC上,点F在边AB上,EF∥BC,BE与CF交于点O,连接AO交EF于点G,延长AO交BC于点D,求证:BD=CD,EG=FG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
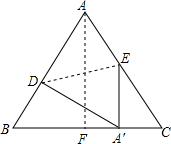 如图,△ABC是正三角形,点E是AC边上的中点,将三角形的一部分沿着DE折叠,使得点A于BC边上的某一点A′重合,若∠BEA′-∠A′EC=∠BAC,求∠ADE.
如图,△ABC是正三角形,点E是AC边上的中点,将三角形的一部分沿着DE折叠,使得点A于BC边上的某一点A′重合,若∠BEA′-∠A′EC=∠BAC,求∠ADE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
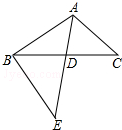 如图,△ABC中,AE交BC于点D,∠C=∠CBE,AD:DE=3:5,BD=4,则DC的长等于( )
如图,△ABC中,AE交BC于点D,∠C=∠CBE,AD:DE=3:5,BD=4,则DC的长等于( )| A. | $\frac{15}{4}$ | B. | $\frac{12}{5}$ | C. | $\frac{20}{3}$ | D. | $\frac{17}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
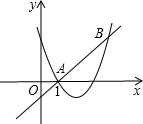 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B,且当x=4时,二次函数的值为6.
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B,且当x=4时,二次函数的值为6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com