练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    抛物线y=-x2可由抛物线y=-(x-2)2+3如何平移得到（    ）
    A．先向左平移2个单位，再向下平移3个单位
    B．先向右平移2个单位，再向下平移3个单位
    C．先向左平移2个单位，再向上平移3个单位
    D．先向右平移2个单位，再向上平移3个单位
    D.

    试题分析：找到两个抛物线的顶点，根据抛物线的顶点即可判断是如何平移得到．
    ∵y=（x-2）2+3的顶点坐标为（2，3），y=-x2的顶点坐标为（0，0），
    ∴将抛物线y=-x2向右平移2个单位，再向上平移3个单位，可得到抛物线y=（x-2）2+3．
    故选D．
    考点: 二次函数图象与几何变换．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：填空题

    二次函数y＝x2－6x＋n的部分图象如图所示，则它的对称轴为 x＝　　　　　．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，抛物线与x轴交于A（1，0）、B（﹣3，0）两点，与y轴交于点C（0，3），设抛物线的顶点为D．

    （1）求该抛物线的解析式与顶点D的坐标．
    （2）试判断△BCD的形状，并说明理由．
    （3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCD相似？若存在，请直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

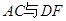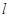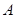    有两个直角三角形，在△ABC中，∠ACB=90°，AC=3，BC=6，在△DEF中，∠FDE=90°，DE=DF=4。将这两个直角三角形按图1所示位置摆放，其中直角边在同一直线上，且点与点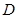重合。现固定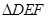，将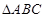以每秒1个单位长度的速度在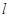上向右平移，当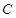点与点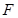重合时运动停止。设平移时间为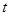秒。

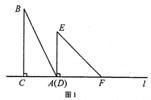
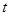    （1）当为       秒时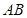，边恰好经过点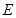；当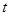为       秒时，运动停止；
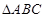    （2）在平移过程中，设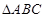与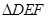重叠部分的面积为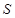，请直接写出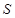与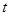的函数关系式，并写出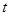的取值范围；
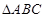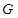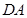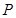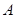    （3）当停止运动后，如图2，为线段上一点，若一动点从点出发，先沿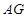方向运动，到达点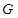后再沿斜坡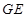方向运动到达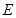点，若该动点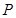在线段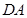上运动的速度是它在斜坡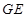上运动速度的2倍，试确定斜坡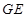的坡度，使得该动点从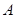点运动到点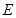所用的时间最短。（要求，简述确定点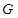位置的方法，但不要求证明。）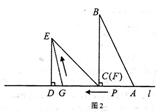

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    将抛物线y1＝2x2向右平移2个单位，得到抛物线y2的图象. P是抛物线y2对称轴上的一个动点，直线x＝t平行于y轴，分别与直线y＝x、抛物线y2交于点A、B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，求满足条件的t的值，则t＝       ．

     

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，在直角坐标系xOy中，二次函数y=x2+（2k﹣1）x+k+1的图象与x轴相交于O、A两点．

    （1）求这个二次函数的解析式；
    （2）在这条抛物线的对称轴右边的图象上有一点B，使△AOB的面积等于6，求点B的坐标；
    （3）对于（2）中的点B，在此抛物线上是否存在点P，使∠POB=90°？若存在，求出点P的坐标，并求出△POB的面积；若不存在，请说明理由

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    在平面直角坐标系中，如果抛物线分别向上、向右平移2个单位，那么新抛物线的解析式是（      ）
    A．B．
    C．D．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    如右图，已知二次函数y=ax2＋bx＋c的图象过A（－3，0），对称轴为直线x=－1，下列结论：①b2>4ac；②2a＋b=0；③a－b＋c=0；④5a<b；⑤a－b>m(am＋b)(m≠－1)其中正确的结论有（     ）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    抛物线上部分点的横坐标ｘ，纵坐标y的对应值如下表：
    ｘ
    		…


    		0
    		1
    		2
    		…
    y
    		…
    		0
    		4
    		6
    		6
    		4
    		…
    由上表可知，下列说法正确的个数是 （       ）
    ①抛物线与ｘ轴的一个交点为　　　②抛物线与轴的交点为
    ③抛物线的对称轴是：　　　　　　 ④在对称轴左侧y随ｘ增大而增大
    A．1　　　　　Ｂ．2　　　　　Ｃ．3　　　　　Ｄ．4

    查看答案和解析>>

    同步练习册答案