
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
(1)求证:∠ACM=∠ABC;
(2)延长BC到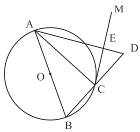 D,使BC = CD,连接AD与CM交于点E,若⊙O的半径为3
D,使BC = CD,连接AD与CM交于点E,若⊙O的半径为3 ,ED = 2,
,ED = 2,  求∆ACE的外接圆的半径.
求∆ACE的外接圆的半径.
证明:(1)连接OC
∵ AB为⊙O的直径
∴ ∠ACB = 90°
∴ ∠ABC +∠BAC = 90°[来源:]
又∵ CM是⊙O的切线
∴ OC⊥CM
∴ ∠ACM +∠ACO = 90°
∵ CO = AO
∴ ∠BAC =∠ACO
∴ ∠ACM =∠ABC
(2)∵ BC = CD
∴ OC∥AD
又∵ OC⊥CE
∴ AD⊥CE
∴ ΔAEC是直角三角形
∴ ΔAEC的外接圆的直径为AC
又∵ ∠ABC +∠BAC = 90°
∠ACM +∠ECD = 90°
而∠ABC =∠ACM
∴ ∠BAC =∠ECD
又∠CED =∠ACB = 90°
∴ ΔABC∽ΔCDE
∴ 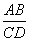 =
= 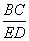
而⊙O的半径为3
∴ AB = 6
∴ 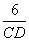 =
= 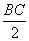
∴ BC2 = 12
∴ BC = 2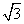 在RtΔABC中
在RtΔABC中
∴ AC = 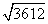 = 2
= 2
∴ ΔAEC的外接圆的半径为


科目:初中数学 来源: 题型:
今年我市有4万名学生参 加中考,为了了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:
加中考,为了了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:
①这4万名考生的数学中考成绩的全体是总体;②每个考生是个体;③2000名考生是总体的一个样本;④样本容量是2000.
其中说法正确的有( )
A.4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,则∠E1D1B的度数为( )
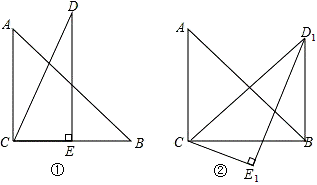
A.10° B. 20° C. 7.5° D. 15°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com