
【题目】已知等边△ABC的边长为12,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )
A.3
B.4
C.8
D.9
【答案】C
【解析】解:如图, 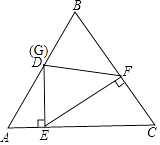
设BD=x,
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵DE⊥AC于点E,EF⊥BC于点F,FG⊥AB,
∴∠BDF=∠DEA=∠EFC=90°,
∴BF=2x,
∴CF=12﹣2x,
∴CE=2CF=24﹣4x,
∴AE=12﹣CE=4x﹣12,
∴AD=2AE=8x﹣24,
∵AD+BD=AB,
∴8x﹣24+x=12,
∴x=4,
∴AD=8x﹣24=32﹣24=8.
故选C.
【考点精析】通过灵活运用等边三角形的性质和含30度角的直角三角形,掌握等边三角形的三个角都相等并且每个角都是60°;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半即可以解答此题.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(1)求抛物线的解析式;
(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点N从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN的面积为S,点M运动时间为t,试求S与t的函数关系,并求S的最大值;
(3)在点M运动过程中,是否存在某一时刻t,使△MBN为直角三角形?若存在,求出t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF= ![]() CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( ) 
A.6
B.4
C.7
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负. 如果小王和小张按上述规则各转动转盘一次,则
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多30元,用500元购得的排球数量与用800元购得的足球数量相等.
(1)排球和足球的单价各是多少元?
(2)若恰好用去1200元,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:用“十字相乘法”分解因式2x2﹣x﹣3的方法.
(i)二次项系数2=1×2;
(ii)常数项﹣3=﹣1×3=1×(﹣3),验算:“交叉相乘之和”;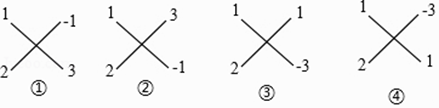
1×3+2×(﹣1)=1 1×(﹣1)+2×3=5 1×(﹣3)+2×1=﹣1 1×1+2×(﹣3)=﹣5
(iii)发现第③个“交叉相乘之和”的结果1×(﹣3)+2×1=﹣1,等于一次项系数﹣1.
即:(x+1)(2x﹣3)=2x2﹣3x+2x﹣3=2x2﹣x﹣3,则2x2﹣x﹣3=(x+1)(2x﹣3).
像这样,通过十字交叉线帮助,把二次三项式分解因式的方法,叫做十字相乘法.仿照以上方法,分解因式:3x2+5x﹣12= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的统计图,已知“查资料”的人数是40人. 
请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是度;
(2)补全条形统计图;
(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com